concept_formation package¶
concept_formation.cobweb module¶
The Cobweb module contains the CobwebTree and CobwebNode
classes which are used to achieve the basic Cobweb functionality.
CobwebTree¶
-
class
concept_formation.cobweb.CobwebTree[source]¶ The CobwebTree contains the knoweldge base of a partiucluar instance of the cobweb algorithm and can be used to fit and categorize instances.
-
categorize(instance)[source]¶ Sort an instance in the categorization tree and return its resulting concept.
The instance is passed down the categorization tree according to the normal cobweb algorithm except using only the best operator and without modifying nodes’ probability tables. This process does not modify the tree’s knowledge for a modifying version of labeling use the
CobwebTree.ifit()functionParameters: instance (Instance) – an instance to be categorized into the tree. Returns: A concept describing the instance Return type: CobwebNode See also
-
cobweb(instance)[source]¶ The core cobweb algorithm used in fitting and categorization.
In the general case, the cobweb algorith entertains a number of sorting operations for the instance and then commits to the operation that maximizes the
category utilityof the tree at the current node and then recurses.At each node the alogrithm first calculates the category utility of inserting the instance at each of the node’s children, keeping the best two (see:
CobwebNode.two_best_children), and then calculates the category_utility of performing other operations using the best two children (see:CobwebNode.get_best_operation), commiting to whichever operation results in the highest category utility. In the case of ties an operation is chosen at random.In the base case, i.e. a leaf node, the algorithm checks to see if the current leaf is an exact match to the current node. If it is, then the instance is inserted and the leaf is returned. Otherwise, a new leaf is created.
Note
This function is equivalent to calling
CobwebTree.ifit()but its better to call ifit because it is the polymorphic method siganture between the different cobweb family algorithms.Parameters: instance (Instance) – an instance to incorporate into the tree Returns: a concept describing the instance Return type: CobwebNode See also
-
fit(instances, iterations=1, randomize_first=True)[source]¶ Fit a collection of instances into the tree.
This is a batch version of the ifit function that takes a collection of instances and categorizes all of them. The instances can be incorporated multiple times to burn in the tree with prior knowledge. Each iteration of fitting uses a randomized order but the first pass can be done in the original order of the list if desired, this is useful for initializing the tree with specific prior experience.
Parameters:
-
ifit(instance)[source]¶ Incrementally fit a new instance into the tree and return its resulting concept.
The instance is passed down the cobweb tree and updates each node to incorporate the instance. This process modifies the tree’s knowledge for a non-modifying version of labeling use the
CobwebTree.categorize()function.Parameters: instance (Instance) – An instance to be categorized into the tree. Returns: A concept describing the instance Return type: CobwebNode See also
-
infer_missing(instance, choice_fn=u'most likely', allow_none=True)[source]¶ Given a tree and an instance, returns a new instance with attribute values picked using the specified choice function (either “most likely” or “sampled”).
Todo
write some kind of test for this.
Parameters: - instance (Instance) – an instance to be completed.
- choice_fn (a string) – a string specifying the choice function to use, either “most likely” or “sampled”.
- allow_none (Boolean) – whether attributes not in the instance can be inferred to be missing. If False, then all attributes will be inferred with some value.
Returns: A completed instance
Return type:
-
CobwebNode¶
-
class
concept_formation.cobweb.CobwebNode(otherNode=None)[source]¶ A CobwebNode represents a concept within the knoweldge base of a particular
CobwebTree. Each node contains a probability table that can be used to calculate the probability of different attributes given the concept that the node represents.In general the
CobwebTree.ifit(),CobwebTree.categorize()functions should be used to initially interface with the Cobweb knowledge base and then the returned concept can be used to calculate probabilities of certain attributes or determine concept labels.This constructor creates a CobwebNode with default values. It can also be used as a copy constructor to “deepcopy” a node, including all references to other parts of the original node’s CobwebTree.
Parameters: otherNode (CobwebNode) – Another concept node to deepcopy. -
attrs(attr_filter=None)[source]¶ Iterates over the attributes present in the node’s attribute-value table with the option to filter certain types. By default the filter will ignore hidden attributes and yield all others. If the string ‘all’ is provided then all attributes will be yielded. In neither of those cases the filter will be interpreted as a function that returns true if an attribute should be yielded and false otherwise.
-
category_utility()[source]¶ Return the category utility of a particular division of a concept into its children.
Category utility is always calculated in reference to a parent node and its own children. This is used as the heuristic to guide the concept formation process. Category Utility is calculated as:
\[CU(\{C_1, C_2, \cdots, C_n\}) = \frac{1}{n} \sum_{k=1}^n P(C_k) \left[ \sum_i \sum_j P(A_i = V_{ij} | C_k)^2 \right] - \sum_i \sum_j P(A_i = V_{ij})^2\]where \(n\) is the numer of children concepts to the current node, \(P(C_k)\) is the probability of a concept given the current node, \(P(A_i = V_{ij} | C_k)\) is the probability of a particular attribute value given the concept \(C_k\), and \(P(A_i = V_{ij})\) is the probability of a particular attribute value given the current node.
In general this is used as an internal function of the cobweb algorithm but there may be times when it would be useful to call outside of the algorithm itself.
Returns: The category utility of the current node with respect to its children. Return type: float
-
compute_relative_CU_const(instance)[source]¶ Computes the constant value that is used to convert between CU and relative CU scores. The constant value is basically the category utility that results from adding the instance to the root, but none of the children. It can be computed directly as:
\[const = \frac{1}{n} \sum_{k=1}^{n} \left[ \frac{C_k.count}{count + 1} \sum_i \sum_j P(A_i = V_{ij} | C)^2 \right] - \sum_i \sum_j P(A_i = V_{ij} | UpdatedRoot)^2\]where \(n\) is the number of children of the root, \(C_k\) is child \(k\), \(C_k.count\) is the number of instances stored in child \(C_k\), \(count\) is the number of instances stored in the root. Finally, \(UpdatedRoot\) is a copy of the root that has been updated with the counts of the instance.
Parameters: instance (Instance) – The instance currently being categorized Returns: The value of the constant used to relativize the CU. Return type: float
-
create_child_with_current_counts()[source]¶ Create a new child (to the current node) with the counts initialized by the current node’s counts.
This operation is used in the speical case of a fringe split when a new node is created at a leaf.
Returns: The new child Return type: CobwebNode
-
create_new_child(instance)[source]¶ Create a new child (to the current node) with the counts initialized by the given instance.
This is the operation used for creating a new child to a node and adding the instance to it.
Parameters: instance (Instance) – The instance currently being categorized Returns: The new child Return type: CobwebNode
-
cu_for_fringe_split(instance)[source]¶ Return the category utility of performing a fringe split (i.e., adding a leaf to a leaf).
A “fringe split” is essentially a new operation performed at a leaf. It is necessary to have the distinction because unlike a normal split a fringe split must also push the parent down to maintain a proper tree structure. This is useful for identifying unnecessary fringe splits, when the two leaves are essentially identical. It can be used to keep the tree from growing and to increase the tree’s predictive accuracy.
Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility of fringe splitting at the current node. Return type: float See also
-
cu_for_insert(child, instance)[source]¶ Compute the category utility of adding the instance to the specified child.
This operation does not actually insert the instance into the child it only calculates what the result of the insertion would be. For the actual insertion function see:
CobwebNode.increment_counts()This is the function used to determine the best children for each of the other operations.Parameters: - child (CobwebNode) – a child of the current node
- instance (Instance) – The instance currently being categorized
Returns: the category utility of adding the instance to the given node
Return type: float
-
cu_for_merge(best1, best2, instance)[source]¶ Return the category utility for merging the two best children.
This does not actually merge the two children it only calculates what the result of the merge would be. For the actual merge operation see:
CobwebNode.merge()Parameters: - best1 (CobwebNode) – The child of the current node with the best category utility
- best2 (CobwebNode) – The child of the current node with the second best category utility
- instance (Instance) – The instance currently being categorized
Returns: The category utility that would result from merging best1 and best2.
Return type: float
See also
-
cu_for_new_child(instance)[source]¶ Return the category utility for creating a new child using the particular instance.
This operation does not actually create the child it only calculates what the result of creating it would be. For the actual new function see:
CobwebNode.create_new_child().Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility of adding the instance to a new child. Return type: float See also
-
cu_for_split(best)[source]¶ Return the category utility for splitting the best child.
This does not actually split the child it only calculates what the result of the split would be. For the actual split operation see:
CobwebNode.split(). Unlike the category utility calculations for the other operations split does not need the instance because splits trigger a recursive call on the current node.Parameters: best (CobwebNode) – The child of the current node with the best category utility Returns: The category utility that would result from splitting best Return type: float See also
-
depth()[source]¶ Returns the depth of the current node in its tree
Returns: the depth of the current node in its tree Return type: int
-
expected_correct_guesses()[source]¶ Returns the number of correct guesses that are expected from the given concept.
This is the sum of the probability of each attribute value squared. This function is used in calculating category utility.
Returns: the number of correct guesses that are expected from the given concept. Return type: float
-
gensym()[source]¶ Generate a unique id and increment the class _counter.
This is used to create a unique name for every concept. As long as the class _counter variable is never externally altered these keys will remain unique.
-
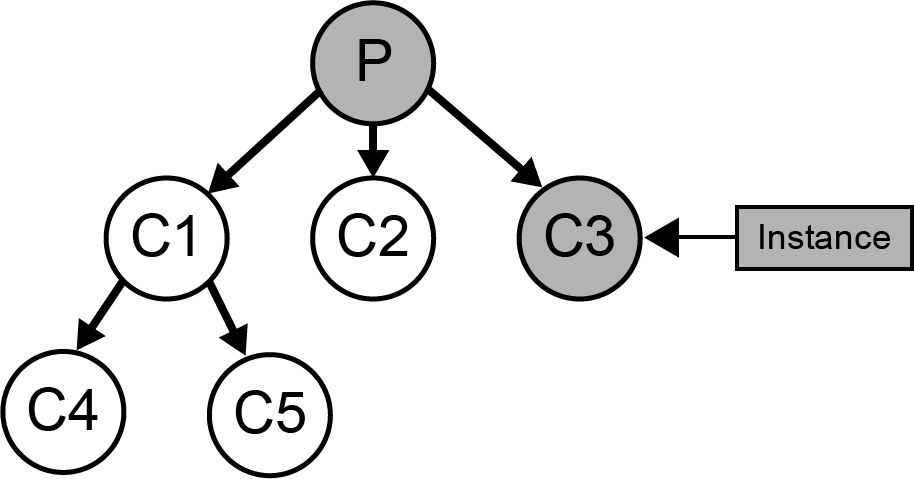
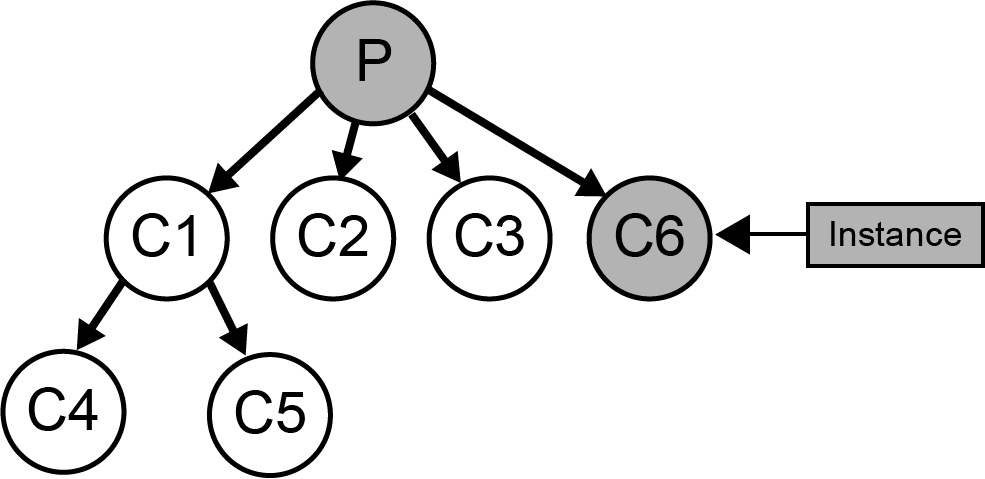
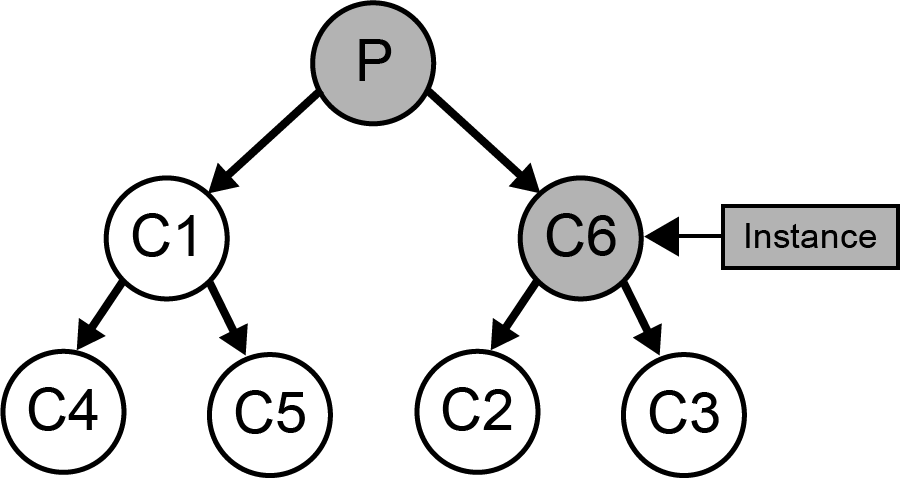
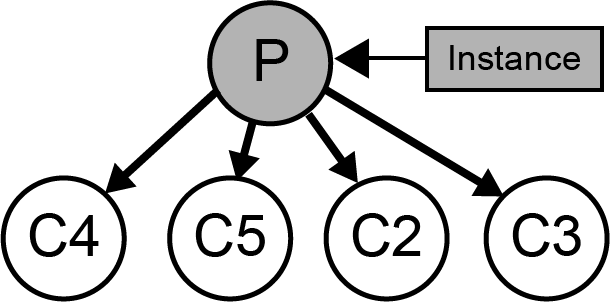
get_best_operation(instance, best1, best2, best1_cu, possible_ops=[u'best', u'new', u'merge', u'split'])[source]¶ Given an instance, the two best children based on category utility and a set of possible operations, find the operation that produces the highest category utility, and then return the category utility and name for the best operation. In the case of ties, an operator is randomly chosen.
Given the following starting tree the results of the 4 standard Cobweb operations are shown below:
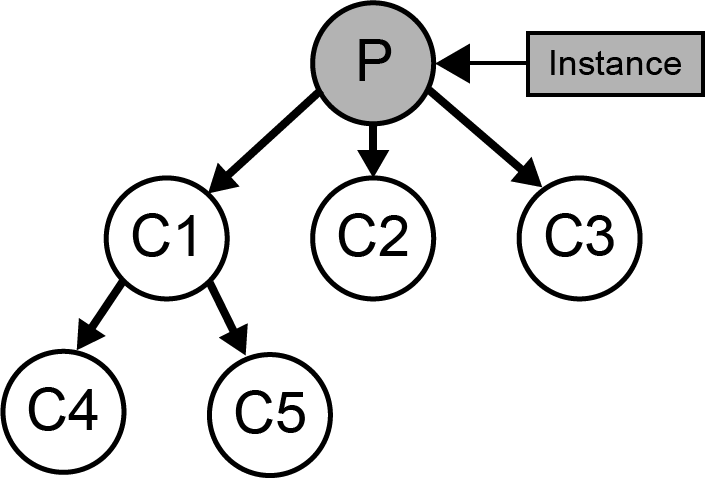
Best - Categorize the instance to child with the best category utility. This results in a recurisve call to
cobweb.New - Create a new child node to the current node and add the instance there. See:
create_new_child.Merge - Take the two best children, create a new node as their mutual parent and add the instance there. See:
merge.Split - Take the best node and promote its children to be children of the current node and recurse on the current node. See:
split
Each operation is entertained and the resultant category utility is used to pick which operation to perform. The list of operations to entertain can be controlled with the possible_ops parameter. For example, when performing categorization without modifying knoweldge only the best and new operators are used.
Parameters: - instance (Instance) – The instance currently being categorized
- best1 ((float, CobwebNode)) – A tuple containing the relative cu of the best child and
the child itself, as determined by
CobwebNode.two_best_children(). - best2 ((float, CobwebNode)) – A tuple containing the relative cu of the second best
child and the child itself, as determined by
CobwebNode.two_best_children(). - possible_ops (["best", "new", "merge", "split"]) – A list of operations from [“best”, “new”, “merge”, “split”] to entertain.
Returns: A tuple of the category utility of the best operation and the name of the best operation.
Return type: (cu_bestOp, name_bestOp)
-
get_weighted_values(attr, allow_none=True)[source]¶ Return a list of weighted choices for an attribute based on the node’s probability table.
This calculation will include an option for the change that an attribute is missing from an instance all together. This is useful for probability and sampling calculations. If the attribute has never appeared in the tree then it will return a 100% chance of None.
Parameters: - attr (Attribute) – an attribute of an instance
- allow_none (Boolean) – whether attributes in the nodes probability table can be inferred to be missing. If False, then None will not be cosidered as a possible value.
Returns: a list of weighted choices for attr’s value
Return type:
-
increment_counts(instance)[source]¶ Increment the counts at the current node according to the specified instance.
Parameters: instance (Instance) – A new instances to incorporate into the node.
-
is_exact_match(instance)[source]¶ Returns true if the concept exactly matches the instance.
Parameters: instance (Instance) – The instance currently being categorized Returns: whether the instance perfectly matches the concept Return type: boolean See also
-
is_parent(other_concept)[source]¶ Return True if this concept is a parent of other_concept
Returns: Trueif this concept is a parent of other_concept elseFalseReturn type: bool
-
log_likelihood(child_leaf)[source]¶ Returns the log-likelihood of a leaf contained within the current concept. Note, if the leaf contains multiple instances, then it is treated as if it contained just a single instance (this function is just called multiple times for each instance in the leaf).
-
merge(best1, best2)[source]¶ Merge the two specified nodes.
A merge operation introduces a new node to be the merger of the the two given nodes. This new node becomes a child of the current node and the two given nodes become children of the new node.
Parameters: - best1 (CobwebNode) – The child of the current node with the best category utility
- best2 (CobwebNode) – The child of the current node with the second best category utility
Returns: The new child node that was created by the merge
Return type:
-
num_concepts()[source]¶ Return the number of concepts contained below the current node in the tree.
When called on the
CobwebTree.rootthis is the number of nodes in the whole tree.Returns: the number of concepts below this concept. Return type: int
-
output_json()[source]¶ Outputs the categorization tree in JSON form
Returns: an object that contains all of the structural information of the node and its children Return type: obj
-
predict(attr, choice_fn=u'most likely', allow_none=True)[source]¶ Predict the value of an attribute, using the specified choice function (either the “most likely” value or a “sampled” value).
Parameters: - attr (Attribute) – an attribute of an instance.
- choice_fn (a string) – a string specifying the choice function to use, either “most likely” or “sampled”.
- allow_none (Boolean) – whether attributes not in the instance can be inferred to be missing. If False, then all attributes will be inferred with some value.
Returns: The most likely value for the given attribute in the node’s probability table.
Return type:
-
pretty_print(depth=0)[source]¶ Print the categorization tree
The string formatting inserts tab characters to align child nodes of the same depth.
Parameters: depth (int) – The current depth in the print, intended to be called recursively Returns: a formated string displaying the tree and its children Return type: str
-
probability(attr, val)[source]¶ Returns the probability of a particular attribute value at the current concept. This takes into account the possibilities that an attribute can take any of the values available at the root, or be missing.
If you you want to check if the probability that an attribute is missing, then check for the probability that the val is
None.Parameters: Returns: The probability of attr having the value val in the current concept.
Return type: float
-
relative_cu_for_insert(child, instance)[source]¶ Computes a relative CU score for each insert operation. The relative CU score is more efficient to calculate for each insert operation and is guranteed to have the same rank ordering as the CU score so it can be used to determine which insert operation is best. The relative CU can be computed from the CU using the following transformation.
\[relative_cu(cu) = (cu - const) * n * (count + 1)\]where \(const\) is the one returned by
CobwebNode.compute_relative_CU_const(), \(n\) is the number of children of the current node, and \(count\) is the number of instances stored in the current node (the root).The particular \(const\) value was chosen to make the calculation of the relative cu scores for each insert operation efficient. When computing the CU for inserting the instance into a particular child, the terms in the formula above can be expanded and many of the intermediate calculations cancel out. After these cancelations, computing the relative CU for inserting into a particular child \(C_i\) reduces to:
relative_cu_for_insert(C_i) = (C_i.count + 1) * sum_i sum_j P(A_i = V_{ij}| UpdatedC_i)^2 - (C_i.count) * sum_i sum_j P(A_i = V_{ij}| C_i)^2where \(UpdatedC_i\) is a copy of \(C_i\) that has been updated with the counts from the given instance.
By computing relative_CU scores instead of CU scores for each insert operation, the time complexity of the underlying Cobweb algorithm is reduced from \(O(B^2 \times log_B(n) \times AV)\) to \(O(B \times log_B(n) \times AV)\) where \(B\) is the average branching factor of the tree, :math`n` is the number of instances being categorized, \(A\) is the average number of attributes per instance, and \(V\) is the average number of values per attribute.
Parameters: - child (CobwebNode) – a child of the current node
- instance (Instance) – The instance currently being categorized
Returns: the category utility of adding the instance to the given node
Return type: float
-
shallow_copy()[source]¶ Create a shallow copy of the current node (and not its children)
This can be used to copy only the information relevant to the node’s probability table without maintaining reference to other elements of the tree, except for the root which is necessary to calculate category utility.
-
split(best)[source]¶ Split the best node and promote its children
A split operation removes a child node and promotes its children to be children of the current node. Split operations result in a recursive call of cobweb on the current node so this function does not return anything.
Parameters: best (CobwebNode) – The child node to be split
-
two_best_children(instance)[source]¶ Calculates the category utility of inserting the instance into each of this node’s children and returns the best two. In the event of ties children are sorted first by category utility, then by their size, then by a random value.
Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility and indices for the two best children (the second tuple will be Noneif there is only 1 child).Return type: ((cu_best1,index_best1),(cu_best2,index_best2))
-
update_counts_from_node(node)[source]¶ Increments the counts of the current node by the amount in the specified node.
This function is used as part of copying nodes and in merging nodes.
Parameters: node (CobwebNode) – Another node from the same CobwebTree
-
concept_formation.cobweb3 module¶
The Cobweb3 module contains the Cobweb3Tree and Cobweb3Node
classes, which extend the traditional Cobweb capabilities to support numeric
values on attributes.
Cobweb3Tree¶
-
class
concept_formation.cobweb3.Cobweb3Tree(scaling=0.5, inner_attr_scaling=True)[source]¶ Bases:
concept_formation.cobweb.CobwebTreeThe Cobweb3Tree contains the knowledge base of a partiucluar instance of the Cobweb/3 algorithm and can be used to fit and categorize instances. Cobweb/3’s main difference over Cobweb is the ability to handle numerical attributes by applying an assumption that they should follow a normal distribution. For the purposes of Cobweb/3’s core algorithms a numeric attribute is any value where
isinstance(instance[attr], Number)returnsTrue.The scaling parameter determines whether online normalization of continuous attributes is used, and to what standard deviation the values are scaled to. Scaling divides the std of each attribute by the std of the attribute in the root divided by the scaling constant (i.e., \(\sigma_{root} / scaling\) when making category utility calculations. Scaling is useful to balance the weight of different numerical attributes, without scaling the magnitude of numerical attributes can affect category utility calculation meaning numbers that are naturally larger will recieve preference in the category utility calculation.
Parameters: - scaling (a float greater than 0.0, None, or False) – The number of standard deviations numeric attributes are scaled to. By default this value is 0.5 (half a standard deviation), which is the max std of nominal values. If disabiling scaling is desirable, then it can be set to False or None.
- inner_attr_scaling – Whether to use the inner most attribute name when scaling numeric attributes. For example, if (‘attr’, ‘?o1’) was an attribute, then the inner most attribute would be ‘attr’. When using inner most attributes, some objects might have multiple attributes (i.e., ‘attr’ for different objects) that contribute to the scaling.
- inner_attr_scaling – boolean
-
categorize(instance)¶ Sort an instance in the categorization tree and return its resulting concept.
The instance is passed down the categorization tree according to the normal cobweb algorithm except using only the best operator and without modifying nodes’ probability tables. This process does not modify the tree’s knowledge for a modifying version of labeling use the
CobwebTree.ifit()functionParameters: instance (Instance) – an instance to be categorized into the tree. Returns: A concept describing the instance Return type: CobwebNode See also
CobwebTree.cobweb()
-
cobweb(instance)[source]¶ A modification of the cobweb function to update the scales object first, so that attribute values can be properly scaled.
-
fit(instances, iterations=1, randomize_first=True)¶ Fit a collection of instances into the tree.
This is a batch version of the ifit function that takes a collection of instances and categorizes all of them. The instances can be incorporated multiple times to burn in the tree with prior knowledge. Each iteration of fitting uses a randomized order but the first pass can be done in the original order of the list if desired, this is useful for initializing the tree with specific prior experience.
Parameters:
-
get_inner_attr(attr)[source]¶ Extracts the inner most attribute name from the provided attribute, if the attribute is a tuple and inner_attr_scaling is on. Otherwise it just returns the attribute. This is used to for normalizing attributes.
>>> t = Cobweb3Tree() >>> t.get_inner_attr(('a', '?object1')) 'a' >>> t.get_inner_attr('a') 'a'
-
ifit(instance)[source]¶ Incrementally fit a new instance into the tree and return its resulting concept.
The cobweb3 version of the
CobwebTree.ifit()function. This version keeps track of all of the continuousParameters: instance (Instance) – An instance to be categorized into the tree. Returns: A concept describing the instance Return type: Cobweb3Node See also
CobwebTree.cobweb()
-
infer_missing(instance, choice_fn=u'most likely', allow_none=True)¶ Given a tree and an instance, returns a new instance with attribute values picked using the specified choice function (either “most likely” or “sampled”).
Todo
write some kind of test for this.
Parameters: - instance (Instance) – an instance to be completed.
- choice_fn (a string) – a string specifying the choice function to use, either “most likely” or “sampled”.
- allow_none (Boolean) – whether attributes not in the instance can be inferred to be missing. If False, then all attributes will be inferred with some value.
Returns: A completed instance
Return type:
Cobweb3Node¶
-
class
concept_formation.cobweb3.Cobweb3Node(otherNode=None)[source]¶ Bases:
concept_formation.cobweb.CobwebNodeA Cobweb3Node represents a concept within the knoweldge base of a particular
Cobweb3Tree. Each node contians a probability table that can be used to calculate the probability of different attributes given the concept that the node represents.In general the
Cobweb3Tree.ifit(),Cobweb3Tree.categorize()functions should be used to initially interface with the Cobweb/3 knowledge base and then the returned concept can be used to calculate probabilities of certain attributes or determine concept labels.-
attrs(attr_filter=None)¶ Iterates over the attributes present in the node’s attribute-value table with the option to filter certain types. By default the filter will ignore hidden attributes and yield all others. If the string ‘all’ is provided then all attributes will be yielded. In neither of those cases the filter will be interpreted as a function that returns true if an attribute should be yielded and false otherwise.
-
category_utility()¶ Return the category utility of a particular division of a concept into its children.
Category utility is always calculated in reference to a parent node and its own children. This is used as the heuristic to guide the concept formation process. Category Utility is calculated as:
\[CU(\{C_1, C_2, \cdots, C_n\}) = \frac{1}{n} \sum_{k=1}^n P(C_k) \left[ \sum_i \sum_j P(A_i = V_{ij} | C_k)^2 \right] - \sum_i \sum_j P(A_i = V_{ij})^2\]where \(n\) is the numer of children concepts to the current node, \(P(C_k)\) is the probability of a concept given the current node, \(P(A_i = V_{ij} | C_k)\) is the probability of a particular attribute value given the concept \(C_k\), and \(P(A_i = V_{ij})\) is the probability of a particular attribute value given the current node.
In general this is used as an internal function of the cobweb algorithm but there may be times when it would be useful to call outside of the algorithm itself.
Returns: The category utility of the current node with respect to its children. Return type: float
-
compute_relative_CU_const(instance)¶ Computes the constant value that is used to convert between CU and relative CU scores. The constant value is basically the category utility that results from adding the instance to the root, but none of the children. It can be computed directly as:
\[const = \frac{1}{n} \sum_{k=1}^{n} \left[ \frac{C_k.count}{count + 1} \sum_i \sum_j P(A_i = V_{ij} | C)^2 \right] - \sum_i \sum_j P(A_i = V_{ij} | UpdatedRoot)^2\]where \(n\) is the number of children of the root, \(C_k\) is child \(k\), \(C_k.count\) is the number of instances stored in child \(C_k\), \(count\) is the number of instances stored in the root. Finally, \(UpdatedRoot\) is a copy of the root that has been updated with the counts of the instance.
Parameters: instance (Instance) – The instance currently being categorized Returns: The value of the constant used to relativize the CU. Return type: float
-
create_child_with_current_counts()¶ Create a new child (to the current node) with the counts initialized by the current node’s counts.
This operation is used in the speical case of a fringe split when a new node is created at a leaf.
Returns: The new child Return type: CobwebNode
-
create_new_child(instance)¶ Create a new child (to the current node) with the counts initialized by the given instance.
This is the operation used for creating a new child to a node and adding the instance to it.
Parameters: instance (Instance) – The instance currently being categorized Returns: The new child Return type: CobwebNode
-
cu_for_fringe_split(instance)¶ Return the category utility of performing a fringe split (i.e., adding a leaf to a leaf).
A “fringe split” is essentially a new operation performed at a leaf. It is necessary to have the distinction because unlike a normal split a fringe split must also push the parent down to maintain a proper tree structure. This is useful for identifying unnecessary fringe splits, when the two leaves are essentially identical. It can be used to keep the tree from growing and to increase the tree’s predictive accuracy.
Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility of fringe splitting at the current node. Return type: float See also
CobwebNode.get_best_operation()
-
cu_for_insert(child, instance)¶ Compute the category utility of adding the instance to the specified child.
This operation does not actually insert the instance into the child it only calculates what the result of the insertion would be. For the actual insertion function see:
CobwebNode.increment_counts()This is the function used to determine the best children for each of the other operations.Parameters: - child (CobwebNode) – a child of the current node
- instance (Instance) – The instance currently being categorized
Returns: the category utility of adding the instance to the given node
Return type: float
See also
CobwebNode.two_best_children()andCobwebNode.get_best_operation()
-
cu_for_merge(best1, best2, instance)¶ Return the category utility for merging the two best children.
This does not actually merge the two children it only calculates what the result of the merge would be. For the actual merge operation see:
CobwebNode.merge()Parameters: - best1 (CobwebNode) – The child of the current node with the best category utility
- best2 (CobwebNode) – The child of the current node with the second best category utility
- instance (Instance) – The instance currently being categorized
Returns: The category utility that would result from merging best1 and best2.
Return type: float
See also
CobwebNode.get_best_operation()
-
cu_for_new_child(instance)¶ Return the category utility for creating a new child using the particular instance.
This operation does not actually create the child it only calculates what the result of creating it would be. For the actual new function see:
CobwebNode.create_new_child().Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility of adding the instance to a new child. Return type: float See also
CobwebNode.get_best_operation()
-
cu_for_split(best)¶ Return the category utility for splitting the best child.
This does not actually split the child it only calculates what the result of the split would be. For the actual split operation see:
CobwebNode.split(). Unlike the category utility calculations for the other operations split does not need the instance because splits trigger a recursive call on the current node.Parameters: best (CobwebNode) – The child of the current node with the best category utility Returns: The category utility that would result from splitting best Return type: float See also
CobwebNode.get_best_operation()
-
depth()¶ Returns the depth of the current node in its tree
Returns: the depth of the current node in its tree Return type: int
-
expected_correct_guesses()[source]¶ Returns the number of attribute values that would be correctly guessed in the current concept. This extension supports both nominal and numeric attribute values.
The typical Cobweb/3 calculation for correct guesses is:
\[P(A_i = V_{ij})^2 = \frac{1}{2 * \sqrt{\pi} * \sigma}\]However, this does not take into account situations when \(P(A_i) < 1.0\). Additionally, the original formulation set \(\sigma\) to have a user specified minimum value. However, for small lower bounds, this lets cobweb achieve more than 1 expected correct guess per attribute, which is impossible for nominal attributes (and does not really make sense for continuous either). This causes problems when both nominal and continuous values are being used together; i.e., continuous attributes will get higher preference.
To account for this we use a modified equation:
\[P(A_i = V_{ij})^2 = P(A_i)^2 * \frac{1}{2 * \sqrt{\pi} * \sigma}\]The key change here is that we multiply by \(P(A_i)^2\). Further, instead of bounding \(\sigma\) by a user specified lower bound (often called acuity), we add some independent, normally distributed noise to sigma: \(\sigma = \sqrt{\sigma^2 + \sigma_{noise}^2}\), where \(\sigma_{noise} = \frac{1}{2 * \sqrt{\pi}}\). This ensures the expected correct guesses never exceeds 1. From a theoretical point of view, it basically is an assumption that there is some independent, normally distributed measurement error that is added to the estimated error of the attribute (https://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables). It is possible that there is additional measurement error, but the value is chosen so as to yield a sensical upper bound on the expected correct guesses.
Returns: The number of attribute values that would be correctly guessed in the current concept. Return type: float
-
gensym()¶ Generate a unique id and increment the class _counter.
This is used to create a unique name for every concept. As long as the class _counter variable is never externally altered these keys will remain unique.
-
get_best_operation(instance, best1, best2, best1_cu, possible_ops=[u'best', u'new', u'merge', u'split'])¶ Given an instance, the two best children based on category utility and a set of possible operations, find the operation that produces the highest category utility, and then return the category utility and name for the best operation. In the case of ties, an operator is randomly chosen.
Given the following starting tree the results of the 4 standard Cobweb operations are shown below:

Best - Categorize the instance to child with the best category utility. This results in a recurisve call to
cobweb.New - Create a new child node to the current node and add the instance there. See:
create_new_child.Merge - Take the two best children, create a new node as their mutual parent and add the instance there. See:
merge.Split - Take the best node and promote its children to be children of the current node and recurse on the current node. See:
split
Each operation is entertained and the resultant category utility is used to pick which operation to perform. The list of operations to entertain can be controlled with the possible_ops parameter. For example, when performing categorization without modifying knoweldge only the best and new operators are used.
Parameters: - instance (Instance) – The instance currently being categorized
- best1 ((float, CobwebNode)) – A tuple containing the relative cu of the best child and
the child itself, as determined by
CobwebNode.two_best_children(). - best2 ((float, CobwebNode)) – A tuple containing the relative cu of the second best
child and the child itself, as determined by
CobwebNode.two_best_children(). - possible_ops (["best", "new", "merge", "split"]) – A list of operations from [“best”, “new”, “merge”, “split”] to entertain.
Returns: A tuple of the category utility of the best operation and the name of the best operation.
Return type: (cu_bestOp, name_bestOp)
-
get_weighted_values(attr, allow_none=True)[source]¶ Return a list of weighted choices for an attribute based on the node’s probability table.
This calculation will include an option for the change that an attribute is missing from an instance all together. This is useful for probability and sampling calculations. If the attribute has never appeared in the tree then it will return a 100% chance of None.
Parameters: - attr (Attribute) – an attribute of an instance
- allow_none (Boolean) – whether attributes in the nodes probability table can be inferred to be missing. If False, then None will not be cosidered as a possible value.
Returns: a list of weighted choices for attr’s value
Return type:
-
increment_counts(instance)[source]¶ Increment the counts at the current node according to the specified instance.
Cobweb3Node uses a modified version of
CobwebNode.increment_countsthat handles numerical attributes properly. Any attribute value whereisinstance(instance[attr], Number)returnsTruewill be treated as a numerical attribute and included under an assumption that the number should follow a normal distribution.Warning
If a numeric attribute is found in an instance with the name of a previously nominal attribute, or vice versa, this function will raise an exception. See:
NumericToNominalfor a way to fix this error.Parameters: instance (Instance) – A new instances to incorporate into the node.
-
is_exact_match(instance)[source]¶ Returns true if the concept exactly matches the instance.
Parameters: instance (Instance) – The instance currently being categorized Returns: whether the instance perfectly matches the concept Return type: boolean See also
CobwebNode.get_best_operation()
-
is_parent(other_concept)¶ Return True if this concept is a parent of other_concept
Returns: Trueif this concept is a parent of other_concept elseFalseReturn type: bool
-
log_likelihood(child_leaf)[source]¶ Returns the log-likelihood of a leaf contained within the current concept. Note, if the leaf contains multiple instances, then it is treated as if it contained just a single instance (this function is just called multiple times for each instance in the leaf).
-
merge(best1, best2)¶ Merge the two specified nodes.
A merge operation introduces a new node to be the merger of the the two given nodes. This new node becomes a child of the current node and the two given nodes become children of the new node.
Parameters: - best1 (CobwebNode) – The child of the current node with the best category utility
- best2 (CobwebNode) – The child of the current node with the second best category utility
Returns: The new child node that was created by the merge
Return type:
-
num_concepts()¶ Return the number of concepts contained below the current node in the tree.
When called on the
CobwebTree.rootthis is the number of nodes in the whole tree.Returns: the number of concepts below this concept. Return type: int
-
output_json()[source]¶ Outputs the categorization tree in JSON form.
This is a modification of the
CobwebNode.output_jsonto handle numeric values.Returns: an object that contains all of the structural information of the node and its children Return type: obj
-
predict(attr, choice_fn=u'most likely', allow_none=True)[source]¶ Predict the value of an attribute, using the provided strategy.
If the attribute is a nominal then this function behaves the same as
CobwebNode.predict. If the attribute is numeric then the mean value from theContinuousValueis chosen.Parameters: - attr (Attribute) – an attribute of an instance.
- allow_none (Boolean) – whether attributes not in the instance can be inferred to be missing. If False, then all attributes will be inferred with some value.
Returns: The most likely value for the given attribute in the node’s probability table.
Return type:
-
pretty_print(depth=0)[source]¶ Print the categorization tree
The string formatting inserts tab characters to align child nodes of the same depth. Numerical values are printed with their means and standard deviations.
Parameters: depth (int) – The current depth in the print, intended to be called recursively Returns: a formated string displaying the tree and its children Return type: str
-
probability(attr, val)[source]¶ Returns the probability of a particular attribute value at the current concept.
This takes into account the possibilities that an attribute can take any of the values available at the root, or be missing.
For numerical attributes it returns the integral of the product of two gaussians. One gaussian has \(\mu = val\) and \(\sigma = \sigma_{noise} = \frac{1}{2 * \sqrt{\pi}}\) (where \(\sigma_{noise}\) is from
Cobweb3Node.expected_correct_guessesand ensures the probability or expected correct guesses never exceeds 1). The second gaussian has the mean ad std values from the current concept with additional gaussian noise (independent and normally distributed noise with \(\sigma_{noise} = \frac{1}{2 * \sqrt{\pi}}\)).The integral of this gaussian product is another gaussian with \(\mu\) equal to the concept attribut mean and \(\sigma = \sqrt{\sigma_{attr}^2 + 2 * \sigma_{noise}^2}\) or, slightly simplified, \(\sigma = \sqrt{\sigma_{attr}^2 + 2 * \frac{1}{2 * \pi}}\).
Parameters: Returns: The probability of attr having the value val in the current concept.
Return type: float
-
relative_cu_for_insert(child, instance)¶ Computes a relative CU score for each insert operation. The relative CU score is more efficient to calculate for each insert operation and is guranteed to have the same rank ordering as the CU score so it can be used to determine which insert operation is best. The relative CU can be computed from the CU using the following transformation.
\[relative_cu(cu) = (cu - const) * n * (count + 1)\]where \(const\) is the one returned by
CobwebNode.compute_relative_CU_const(), \(n\) is the number of children of the current node, and \(count\) is the number of instances stored in the current node (the root).The particular \(const\) value was chosen to make the calculation of the relative cu scores for each insert operation efficient. When computing the CU for inserting the instance into a particular child, the terms in the formula above can be expanded and many of the intermediate calculations cancel out. After these cancelations, computing the relative CU for inserting into a particular child \(C_i\) reduces to:
relative_cu_for_insert(C_i) = (C_i.count + 1) * sum_i sum_j P(A_i = V_{ij}| UpdatedC_i)^2 - (C_i.count) * sum_i sum_j P(A_i = V_{ij}| C_i)^2where \(UpdatedC_i\) is a copy of \(C_i\) that has been updated with the counts from the given instance.
By computing relative_CU scores instead of CU scores for each insert operation, the time complexity of the underlying Cobweb algorithm is reduced from \(O(B^2 \times log_B(n) \times AV)\) to \(O(B \times log_B(n) \times AV)\) where \(B\) is the average branching factor of the tree, :math`n` is the number of instances being categorized, \(A\) is the average number of attributes per instance, and \(V\) is the average number of values per attribute.
Parameters: - child (CobwebNode) – a child of the current node
- instance (Instance) – The instance currently being categorized
Returns: the category utility of adding the instance to the given node
Return type: float
-
shallow_copy()¶ Create a shallow copy of the current node (and not its children)
This can be used to copy only the information relevant to the node’s probability table without maintaining reference to other elements of the tree, except for the root which is necessary to calculate category utility.
-
split(best)¶ Split the best node and promote its children
A split operation removes a child node and promotes its children to be children of the current node. Split operations result in a recursive call of cobweb on the current node so this function does not return anything.
Parameters: best (CobwebNode) – The child node to be split
-
two_best_children(instance)¶ Calculates the category utility of inserting the instance into each of this node’s children and returns the best two. In the event of ties children are sorted first by category utility, then by their size, then by a random value.
Parameters: instance (Instance) – The instance currently being categorized Returns: the category utility and indices for the two best children (the second tuple will be Noneif there is only 1 child).Return type: ((cu_best1,index_best1),(cu_best2,index_best2))
-
update_counts_from_node(node)[source]¶ Increments the counts of the current node by the amount in the specified node, modified to handle numbers.
Warning
If a numeric attribute is found in an instance with the name of a previously nominal attribute, or vice versa, this function will raise an exception. See:
NumericToNominalfor a way to fix this error.Parameters: node (Cobweb3Node) – Another node from the same Cobweb3Tree
-
concept_formation.trestle module¶
The Trestle module contains the TrestleTree class, which extends
Cobweb3 to support component and relational attributes.
TrestleTree¶
-
class
concept_formation.trestle.TrestleTree(scaling=0.5, inner_attr_scaling=True)[source]¶ Bases:
concept_formation.cobweb3.Cobweb3TreeThe TrestleTree instantiates the Trestle algorithm, which can be used to learn from and categorize instances. Trestle adds the ability to handle component attributes as well as relations in addition to the numerical and nominal attributes of Cobweb and Cobweb/3.
The scaling parameter determines whether online normalization of continuous attributes is used, and to what standard deviation the values are scaled to. Scaling divides the std of each attribute by the std of the attribute in the root divided by the scaling constant (i.e., \(\sigma_{root} / scaling\) when making category utility calculations. Scaling is useful to balance the weight of different numerical attributes, without scaling the magnitude of numerical attributes can affect category utility calculation meaning numbers that are naturally larger will recieve preference in the category utility calculation.
Parameters: - scaling (a float greater than 0.0, None, or False) – The number of standard deviations numeric attributes are scaled to. By default this value is 0.5 (half a standard deviation), which is the max std of nominal values. If disabiling scaling is desirable, then it can be set to False or None.
- inner_attr_scaling – Whether to use the inner most attribute name when scaling numeric attributes. For example, if (‘attr’, ‘?o1’) was an attribute, then the inner most attribute would be ‘attr’. When using inner most attributes, some objects might have multiple attributes (i.e., ‘attr’ for different objects) that contribute to the scaling.
- inner_attr_scaling – boolean
- structure_map_internally (boolean) – Determines whether structure mapping is used at each node during categorization (and when merging), this drastically reduces performance, but allows the category structure to influcence structure mapping.
-
categorize(instance)[source]¶ Sort an instance in the categorization tree and return its resulting concept.
The instance is passed down the the categorization tree according to the normal cobweb algorithm except using only the new and best opperators and without modifying nodes’ probability tables. This does not modify the tree’s knowledge base for a modifying version see
TrestleTree.ifit()This version differs fomr the normal
CobwebTree.categorizeandCobweb3Tree.categorizeby structure mapping instances before categorizing them.Parameters: instance (Instance) – an instance to be categorized into the tree. Returns: A concept describing the instance Return type: CobwebNode See also
-
cobweb(instance)¶ A modification of the cobweb function to update the scales object first, so that attribute values can be properly scaled.
-
fit(instances, iterations=1, randomize_first=True)¶ Fit a collection of instances into the tree.
This is a batch version of the ifit function that takes a collection of instances and categorizes all of them. The instances can be incorporated multiple times to burn in the tree with prior knowledge. Each iteration of fitting uses a randomized order but the first pass can be done in the original order of the list if desired, this is useful for initializing the tree with specific prior experience.
Parameters:
-
gensym()[source]¶ Generates unique names for naming renaming apart objects.
Returns: a unique object name Return type: ‘?o’+counter
-
get_inner_attr(attr)¶ Extracts the inner most attribute name from the provided attribute, if the attribute is a tuple and inner_attr_scaling is on. Otherwise it just returns the attribute. This is used to for normalizing attributes.
>>> t = Cobweb3Tree() >>> t.get_inner_attr(('a', '?object1')) 'a' >>> t.get_inner_attr('a') 'a'
-
ifit(instance)[source]¶ Incrementally fit a new instance into the tree and return its resulting concept.
The instance is passed down the tree and updates each node to incorporate the instance. This modifies the tree’s knowledge for a non-modifying version see:
TrestleTree.categorize().This version is modified from the normal
CobwebTree.ifitby first structure mapping the instance before fitting it into the knoweldge base.Parameters: instance (Instance) – an instance to be categorized into the tree. Returns: A concept describing the instance Return type: Cobweb3Node See also
-
infer_missing(instance, choice_fn=u'most likely', allow_none=True)[source]¶ Given a tree and an instance, returns a new instance with attribute values picked using the specified choice function (either “most likely” or “sampled”).
Todo
write some kind of test for this.
Parameters: - instance (Instance) – an instance to be completed.
- choice_fn (a string) – a string specifying the choice function to use, either “most likely” or “sampled”.
- allow_none (Boolean) – whether attributes not in the instance can be inferred to be missing. If False, then all attributes will be inferred with some value.
Returns: A completed instance
Return type: instance
-
trestle(instance)[source]¶ The core trestle algorithm used in fitting and categorization.
This function is similar to
Cobweb.cobwebThe key difference between trestle and cobweb is that trestle performs structure mapping (see:structure_map) before proceeding through the normal cobweb algorithm.Parameters: instance (Instance) – an instance to be categorized into the tree. Returns: A concept describing the instance Return type: CobwebNode
-
update_scales(instance)¶ Reads through all the attributes in an instance and updates the tree scales object so that the attributes can be properly scaled.
concept_formation.cluster module¶
The cluster model contains functions computing clustering using CobwebTrees and their derivatives.
-
concept_formation.cluster.AIC(clusters, leaves)[source]¶ Calculates the Akaike Information Criterion of the a given clustering from a given tree and set of instances.
This can be used as one of the heuristic functions in
cluster_split_search().\[AIC = 2k - 2\ln (\mathcal{L})\]- \(\ln(\mathcal{L})\) is the total log-likelihood of the cluster concepts
- \(k\) is the total number of unique attribute value pairs in the tree root times the number of clusters
Parameters: - clusters ({
CobwebNode,CobwebNode, …}) – A unique set of cluster concepts from the tree - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – The tree that the clusters come from (used to calculated number of parameters) - instances ([Instance, Instance, …]) – The set of clustered instances
Returns: The AIC of the clustering
Return type: float
-
concept_formation.cluster.AICc(clusters, leaves)[source]¶ Calculates the Akaike Information Criterion of the a given clustering from a given tree and set of instances with a correction for finite sample sizes.
This can be used as one of the heuristic functions in
cluster_split_search().\[AICc = 2k - 2\ln (\mathcal{L}) + \frac{2k(k+1)}{n-k-1}\]- \(\ln(\mathcal{L})\) is the total log-likelihood of the cluster concepts
- \(k\) is the total number of unique attribute value pairs in the tree root times the number of clusters
- \(n\) is the number of instances.
Given the particular math of AICc I decided that is n-k-1 = 0 then the function will return float(‘inf’).
Parameters: - clusters ({
CobwebNode,CobwebNode, …}) – A unique set of cluster concepts from the tree - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – The tree that the clusters come from (used to calculated number of parameters) - instances ([Instance, Instance, …]) – The set of clustered instances
Returns: The AIC of the clustering
Return type: float
-
concept_formation.cluster.BIC(clusters, leaves)[source]¶ Calculates the Bayesian Information Criterion of the a given clustering from a given tree and set of instances.
This can be used as one of the heuristic functions in
cluster_split_search().\[BIC = k\ln (n) - 2\ln (\mathcal{L})\]- \(\ln(\mathcal{L})\) is the total log-likelihood of the cluster concepts
- \(k\) is the total number of unique attribute value pairs in the tree root times the number of clusters
- \(n\) is the number of instances.
Parameters: - clusters ({
CobwebNode,CobwebNode, …}) – A unique set of cluster concepts from the tree - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – The tree that the clusters come from (used to calculated number of parameters) - instances ([Instance, Instance, …]) – The set of clustered instances
Returns: The BIC of the clustering
Return type: float
-
concept_formation.cluster.CU(cluster, leaves)[source]¶ Calculates the Category Utility of a tree state given clusters and leaves.
This just uses the basic category utility function of a node created from the leave instances. This also negates the result so it can be minimized like the other heuristic functions.
Todo
we might want to do this with infered missing instances rather than leaves
Parameters: - clusters ({
CobwebNode,CobwebNode, …}) – A unique set of cluster concepts from the tree - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – The tree that the clusters come from (used to calculated number of parameters) - instances ([Instance, Instance, …]) – The set of clustered instances
Returns: The CU of the clustering
Return type: float
- clusters ({
-
concept_formation.cluster.cluster(tree, instances, minsplit=1, maxsplit=1, mod=True)[source]¶ Categorize a list of instances into a tree and return a list of flat cluster labelings based on successive splits of the tree.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to be used to generate clusters. - instances ([Instance, Instance, …]) – A list of instances to cluster
- minsplit (int) – The minimum number of splits to perform on the tree
- maxsplit (int) – the maximum number of splits to perform on the tree
- mod (bool) – A flag to determine if instances will be fit (i.e. modifying knoweldge) or categorized (i.e. not modifiying knowledge)
Returns: a list of lists of cluster labels based on successive splits between minsplit and maxsplit.
Return type: [[minsplit clustering], [minsplit+1 clustering], .. [maxsplit clustering]]
See also
- tree (
-
concept_formation.cluster.cluster_iter(tree, instances, heuristic=<function CU>, minsplit=1, maxsplit=100000, mod=True, labels=True)[source]¶ This is the core clustering process that splits the tree according to a given heuristic.
-
concept_formation.cluster.cluster_split_search(tree, instances, heuristic=<function CU>, minsplit=1, maxsplit=1, mod=True, labels=True, verbose=False)[source]¶ Find a clustering of the instances given the tree that is based on successive splittings of the tree in order to minimize some heuristic function.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to be used to generate clusters. - instances ([Instance, Instance, …]) – A list of instances to cluster
- heuristic (a function.) – A heuristic function to minimize in search
- minsplit (int) – The minimum number of splits to perform on the tree
- maxsplit (int) – the maximum number of splits to perform on the tree
- mod (bool) – A flag to determine if instances will be fit (i.e. modifying knoweldge) or categorized (i.e. not modifiying knowledge)
- labels (bool) – A flag to determine whether the process should return a list of cluster labels (true) or a list of concept nodes (false).
- verbose (bool) – If True, the process will print the heuristic at each split as it searches.
Returns: a list of cluster labels based on the optimal number of splits according to the heuristic
Return type: list
See also
- tree (
-
concept_formation.cluster.depth_labels(tree, instances, mod=True)[source]¶ Categorize a list of instances into a tree and return a list of lists of labelings for each instance based on different depth cuts of the tree.
The returned matrix is max(conceptDepth) X len(instances). Labelings are ordered general to specific with final_labels[0] being the root and final_labels[-1] being the leaves.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to be used to generate clusters, it can be pre-trained or newly created. - instances ([Instance, Instance, …]) – A list of instances to cluster
- mod (bool) – A flag to determine if instances will be fit (i.e. modifying knoweldge) or categorized (i.e. not modifiying knowledge)
Returns: a list of lists of cluster labels based on each depth cut of the tree
Return type: [[root labeling], [depth1 labeling], .. [maxdepth labeling]]
- tree (
-
concept_formation.cluster.k_cluster(tree, instances, k=3, mod=True)[source]¶ Categorize a list of instances into a tree and return a flat cluster where
len(set(clustering)) <= k.Clusterings are generated by successively splitting the tree until a split results in a clustering with > k clusters at which point the clustering just before that split is returned. It is possible for this process to return a clustering with < k clusters but not > k clusters.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to be used to generate clusters, it can be pre-trained or newly created. - instances ([Instance, Instance, …]) – A list of instances to cluster
- k (int) – A desired number of clusters to generate
- mod (bool) – A flag to determine if instances will be fit (i.e. modifying knoweldge) or categorized (i.e. not modifiying knowledge)
Returns: a flat cluster labeling
Return type: [label1, label2, ..]
See also
Warning
k must be >= 2.
- tree (
concept_formation.evaluation module¶
The evaluation module contains functions for evaluating the predictive capabilities of CobwebTrees and their derivatives.
-
concept_formation.evaluation.incremental_evaluation(tree, instances, attr, run_length, runs=1, score=<function probability>, randomize_first=True)[source]¶ Given a set of instances and an attribute, perform an incremental prediction task; i.e., try to predict the attribute for each instance before incorporating it into the tree. This will give a type of cross validated result and gives a sense of how performance improves over time.
Incremental evaluation can use different scoring functions depending on the desired evaluation task:
probability()- The probability of the target attribute’s value being present (i.e., accuracy). This is the default scoring function.error()- The difference between the target attribute’s value and the one predicted by the tree’s concept.absolute_error()- Returns the absolute value of the error.squared_error()- Returns the error squared.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to evaluate. - instances ([Instance, Instance, …]) – A list of instances to use for evaluation
- attr (Attribute) – A target instance attribute to use in evaluation.
- run_length (int) – The number of training instances to use within a given run.
- runs (int) – The number of restarted runs to perform
- score (function) – The scoring function to use for evaluation (default probability)
- randomize_first (bool) – Whether to shuffle the first run of instances or not.
Returns: A table that is runs x run_length where each row represents the score for successive instances within a run.
Return type: A table of scores.
-
concept_formation.evaluation.probability(tree, instance, attr, val)[source]¶ Returns the probability of a particular value of an attribute in the instance. One of the scoring functions for incremental_evaluation.
If the instance currently contains the target attribute a shallow copy is created to allow the attribute to be predicted.
Warning
This is an older function in the library and we are not quite sure how to set it up for component values under the new representation and so for the time being it will raise an Exception if it encounts a component.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to evaluate. - instance ({a1:v1, a2:v2, ..}) – An instance to use query the tree with
- attr (Attribute) – A target instance attribute to evaluate probability on
- val (A Nominal or Numeric value.) – The target value of the given attr
Returns: The probabily of the given instance attribute value in the given tree
Return type: float
- tree (
-
concept_formation.evaluation.error(tree, instance, attr, val)[source]¶ Computes the error between the predicted value and the actual value for an attribute. One of the scoring functions for incremental_evaluation.
Warning
We are not quite sure how to compute error or squared for a Numeric values being missing (e.g., 0-1 vs. scale of the numeric value cannot be averaged). So currently, this scoring function raises an Exception when it encounters a missing nunmeric value. We are also not sure how to handle error in the case of Component Values so it will also throw an exception if encounters one of those.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to evaluate. - instance ({a1:v1, a2:v2, ..}) – An instance to use query the tree with
- attr (Attribute) – A target instance attribute to evaluate error on
- val (A Nominal or Numeric value.) – The target value of the given attr
Returns: The error of the given instance attribute value in the given tree
Return type: float, or int in the nominal case.
- tree (
-
concept_formation.evaluation.absolute_error(tree, instance, attr, val)[source]¶ Returns the absolute error of the tree for a particular attribute value pair. One of the scoring functions for incremental_evaluation.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to evaluate. - instance ({a1:v1, a2:v2, ..}) – An instance to use query the tree with
- attr (Attribute) – A target instance attribute to evaluate error on
- val (A Nominal or Numeric value.) – The target value of the given attr
Returns: The error of the given instance attribute value in the given tree
Return type: float, or int in the nominal case.
See also
- tree (
-
concept_formation.evaluation.squared_error(tree, instance, attr, val)[source]¶ Returns the squared error of the tree for a particular attribute value pair. One of the scoring functions for incremental_evaluation.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to evaluate. - instance ({a1:v1, a2:v2, ..}) – An instance to use query the tree with
- attr (Attribute) – A target instance attribute to evaluate error on
- val (A Nominal or Numeric value.) – The target value of the given attr
Returns: The error of the given instance attribute value in the given tree
Return type: float, or int in the nominal case.
See also
- tree (
concept_formation.preprocessor module¶
This module contains an number of proprocessors that can be used on various forms of raw input data to convert an instance into a shape that Trestle would better understand. Almost all preprocessors preserve the original semantics of an instance and are mainly being used to prep for Trestle’s internal operations.
Two abstract preprocessors are defined:
Preprocessor- Defines the general structure of a preprocessor.Pipeline- Allows for chaining a collection of preprocessors together.
Trestle’s normal implementation uses a standard pipeline of preprocessors that run in the following order:
SubComponentProcessor- Pulls any sub-components present in the instance to the top level of the instance and addshas-componentrelations to preserve semantics.Flattener- Flattens component instances into a number of tuples (i.e.(attr,component)) for faster hashing and access.StructureMapper- Gives any variables unique names so they can be renamed in matching without
colliding, and matches instances to the root concept.
The remaining preprocessors are helper classes designed to support data that is not stored in Trestle’s conventional representation:
Tuplizer- Looks for relation attributes denoted as strings (i.e.'(relation e1 e1)') and replaces the string attribute name with the equivalent tuple representation of the relation.ListProcessor- Search for list values and extracts their elements into their own objects and replaces the list with ordering and element-of relations. Intended to preserve the semenatics of a list in JSON representation.ObjectVariablizer- Looks for component objects within an instance and variablizes their names by prepending a'?'.NumericToNominal- Converts numeric values to nominal ones.NominalToNumeric- Converts nominal values to numeric ones.
-
class
concept_formation.preprocessor.ExtractListElements(gensym=None)[source]¶ Bases:
concept_formation.preprocessor.PreprocessorA pre-processor that extracts the elements of lists into their own objects
Find all lists in an instance and extract their elements into their own subjects of the main instance.
This is a first subprocess of the
ListProcessor. None of the list operations are part ofStructureMapper’s standard pipeline.# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> import pprint >>> instance = {“a”: “n”, “list1”: [“test”, {“p”: “q”, “j”: “k”}, {“n”: “m”}]} >>> pp = ExtractListElements() >>> instance = pp.transform(instance) >>> pprint.pprint(instance) {‘?o1’: {‘val’: ‘test’},
‘?o2’: {‘j’: ‘k’, ‘p’: ‘q’}, ‘?o3’: {‘n’: ‘m’}, ‘a’: ‘n’, ‘list1’: [‘?o1’, ‘?o2’, ‘?o3’]}# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> import pprint >>> instance = {“att1”: “V1”, ‘subobj’: {“list1”: [“a”, “b”, “c”, {“B”: “C”, “D”: “E”}]}} >>> pprint.pprint(instance) {‘att1’: ‘V1’, ‘subobj’: {‘list1’: [‘a’, ‘b’, ‘c’, {‘B’: ‘C’, ‘D’: ‘E’}]}} >>> pp = ExtractListElements() >>> instance = pp.transform(instance) >>> pprint.pprint(instance) {‘att1’: ‘V1’,
- ‘subobj’: {‘?o1’: {‘val’: ‘a’},
- ‘?o2’: {‘val’: ‘b’}, ‘?o3’: {‘val’: ‘c’}, ‘?o4’: {‘B’: ‘C’, ‘D’: ‘E’}, ‘list1’: [‘?o1’, ‘?o2’, ‘?o3’, ‘?o4’]}}
>>> instance = pp.undo_transform(instance) >>> pprint.pprint(instance) {'att1': 'V1', 'subobj': {'list1': ['a', 'b', 'c', {'B': 'C', 'D': 'E'}]}}
-
class
concept_formation.preprocessor.Flattener[source]¶ Bases:
concept_formation.preprocessor.PreprocessorFlattens subobject attributes.
Takes an instance that has already been standardized apart and flattens it.
Hierarchy is represented with periods between variable names in the flattened attributes. However, this process converts the attributes with periods in them into a tuple of objects with an attribute as the last element, this is more efficient for later processing.
This is the third and final operation in
StructureMapper’s standard pipeline.>>> import pprint >>> flattener = Flattener() >>> instance = {'a': 1, 'c1': {'b': 1, '_c': 2}} >>> pprint.pprint(instance) {'a': 1, 'c1': {'_c': 2, 'b': 1}} >>> instance = flattener.transform(instance) >>> pprint.pprint(instance) {'a': 1, ('_', ('_c', 'c1')): 2, ('b', 'c1'): 1} >>> instance = flattener.undo_transform(instance) >>> pprint.pprint(instance) {'a': 1, 'c1': {'_c': 2, 'b': 1}}
>>> instance = {'l1': {'l2': {'l3': {'l4': 1}}}} >>> pprint.pprint(instance) {'l1': {'l2': {'l3': {'l4': 1}}}} >>> instance = flattener.transform(instance) >>> pprint.pprint(instance) {('l4', ('l3', ('l2', 'l1'))): 1} >>> instance = flattener.undo_transform(instance) >>> pprint.pprint(instance) {'l1': {'l2': {'l3': {'l4': 1}}}}
-
class
concept_formation.preprocessor.ListProcessor[source]¶ Bases:
concept_formation.preprocessor.PreprocessorPreprocesses out the lists, converting them into objects and relations.
This preprocessor is a pipeline of two operations. First it extracts elements from any lists in the instance and makes them their own subcomponents with unique names. Second it removes the lists altogether and replaces them with a series of relations that both express that subcomponents are elments of the list and the order that they existed in. These two operations transform the list in a way that preserves the semenatics of the original list but makes them compatible with Trestle’s understanding of component objects.
None of the list operations are part of
StructureMapper’s standard pipeline.Warning
The ListProcessor’s undo_transform function is not guaranteed to be deterministic and attempts a best guess at a partial ordering. In most cases this will be fine but in complex instances with multiple lists and user defined ordering relations it can break down. If an ordering cannot be determined then ordering relations are left in place.
# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> import pprint >>> instance = {“att1”: “val1”, “list1”:[“a”, “b”, “a”, “c”, “d”]} >>> lp = ListProcessor() >>> instance = lp.transform(instance) >>> pprint.pprint(instance) {‘?o1’: {‘val’: ‘a’},
‘?o2’: {‘val’: ‘b’}, ‘?o3’: {‘val’: ‘a’}, ‘?o4’: {‘val’: ‘c’}, ‘?o5’: {‘val’: ‘d’}, ‘att1’: ‘val1’, ‘list1’: {}, (‘has-element’, ‘list1’, ‘?o1’): True, (‘has-element’, ‘list1’, ‘?o2’): True, (‘has-element’, ‘list1’, ‘?o3’): True, (‘has-element’, ‘list1’, ‘?o4’): True, (‘has-element’, ‘list1’, ‘?o5’): True, (‘ordered-list’, ‘list1’, ‘?o1’, ‘?o2’): True, (‘ordered-list’, ‘list1’, ‘?o2’, ‘?o3’): True, (‘ordered-list’, ‘list1’, ‘?o3’, ‘?o4’): True, (‘ordered-list’, ‘list1’, ‘?o4’, ‘?o5’): True}>>> instance = lp.undo_transform(instance) >>> pprint.pprint(instance) {'att1': 'val1', 'list1': ['a', 'b', 'a', 'c', 'd']}
# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> instance = {‘l1’: [‘a’, {‘in1’: 3, ‘in2’: 4}, {‘ag’: ‘b’, ‘ah’: ‘c’}, 12, ‘again’]} >>> lp = ListProcessor() >>> instance = lp.transform(instance) >>> pprint.pprint(instance) {‘?o1’: {‘val’: ‘a’},
‘?o2’: {‘in1’: 3, ‘in2’: 4}, ‘?o3’: {‘ag’: ‘b’, ‘ah’: ‘c’}, ‘?o4’: {‘val’: 12}, ‘?o5’: {‘val’: ‘again’}, ‘l1’: {}, (‘has-element’, ‘l1’, ‘?o1’): True, (‘has-element’, ‘l1’, ‘?o2’): True, (‘has-element’, ‘l1’, ‘?o3’): True, (‘has-element’, ‘l1’, ‘?o4’): True, (‘has-element’, ‘l1’, ‘?o5’): True, (‘ordered-list’, ‘l1’, ‘?o1’, ‘?o2’): True, (‘ordered-list’, ‘l1’, ‘?o2’, ‘?o3’): True, (‘ordered-list’, ‘l1’, ‘?o3’, ‘?o4’): True, (‘ordered-list’, ‘l1’, ‘?o4’, ‘?o5’): True}>>> instance = lp.undo_transform(instance) >>> pprint.pprint(instance) {'l1': ['a', {'in1': 3, 'in2': 4}, {'ag': 'b', 'ah': 'c'}, 12, 'again']}
# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> instance = {‘tta’: ‘alpha’, ‘ttb’:{‘tlist’: [‘a’, ‘b’, {‘sub-a’: ‘c’, ‘sub-sub’: {‘s’: ‘d’, ‘sslist’: [‘w’, ‘x’, ‘y’, {‘issue’: ‘here’}]}}, ‘g’]}} >>> pprint.pprint(instance) {‘tta’: ‘alpha’,
- ‘ttb’: {‘tlist’: [‘a’,
‘b’, {‘sub-a’: ‘c’,
- ‘sub-sub’: {‘s’: ‘d’,
- ‘sslist’: [‘w’, ‘x’, ‘y’, {‘issue’: ‘here’}]}},
‘g’]}}
>>> lp = ListProcessor() >>> instance = lp.transform(instance) >>> pprint.pprint(instance) {'tta': 'alpha', 'ttb': {'?o1': {'val': 'a'}, '?o2': {'val': 'b'}, '?o3': {'sub-a': 'c', 'sub-sub': {'?o4': {'val': 'w'}, '?o5': {'val': 'x'}, '?o6': {'val': 'y'}, '?o7': {'issue': 'here'}, 's': 'd', 'sslist': {}}}, '?o8': {'val': 'g'}, 'tlist': {}}, ('has-element', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o4'): True, ('has-element', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o5'): True, ('has-element', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o6'): True, ('has-element', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o7'): True, ('has-element', ('tlist', 'ttb'), '?o1'): True, ('has-element', ('tlist', 'ttb'), '?o2'): True, ('has-element', ('tlist', 'ttb'), '?o3'): True, ('has-element', ('tlist', 'ttb'), '?o8'): True, ('ordered-list', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o4', '?o5'): True, ('ordered-list', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o5', '?o6'): True, ('ordered-list', ('sslist', ('sub-sub', ('?o3', 'ttb'))), '?o6', '?o7'): True, ('ordered-list', ('tlist', 'ttb'), '?o1', '?o2'): True, ('ordered-list', ('tlist', 'ttb'), '?o2', '?o3'): True, ('ordered-list', ('tlist', 'ttb'), '?o3', '?o8'): True}
>>> instance = lp.undo_transform(instance) >>> pprint.pprint(instance) {'tta': 'alpha', 'ttb': {'tlist': ['a', 'b', {'sub-a': 'c', 'sub-sub': {'s': 'd', 'sslist': ['w', 'x', 'y', {'issue': 'here'}]}}, 'g']}}
-
class
concept_formation.preprocessor.ListsToRelations[source]¶ Bases:
concept_formation.preprocessor.PreprocessorConverts an object with lists into an object with sub-objects and list relations.
This is a second subprocess of the
ListProcessor. None of the list operations are part ofStructureMapper’s standard pipeline.# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> ltr = ListsToRelations() >>> import pprint >>> instance = {“list1”: [‘a’, ‘b’, ‘c’]} >>> instance = ltr.transform(instance) >>> pprint.pprint(instance) {‘list1’: {},
(‘has-element’, ‘list1’, ‘a’): True, (‘has-element’, ‘list1’, ‘b’): True, (‘has-element’, ‘list1’, ‘c’): True, (‘ordered-list’, ‘list1’, ‘a’, ‘b’): True, (‘ordered-list’, ‘list1’, ‘b’, ‘c’): True}>>> instance = {"list1": ['a', 'b', 'c'], "list2": ['w', 'x', 'y', 'z']} >>> instance = ltr.transform(instance) >>> pprint.pprint(instance) {'list1': {}, 'list2': {}, ('has-element', 'list1', 'a'): True, ('has-element', 'list1', 'b'): True, ('has-element', 'list1', 'c'): True, ('has-element', 'list2', 'w'): True, ('has-element', 'list2', 'x'): True, ('has-element', 'list2', 'y'): True, ('has-element', 'list2', 'z'): True, ('ordered-list', 'list1', 'a', 'b'): True, ('ordered-list', 'list1', 'b', 'c'): True, ('ordered-list', 'list2', 'w', 'x'): True, ('ordered-list', 'list2', 'x', 'y'): True, ('ordered-list', 'list2', 'y', 'z'): True}
# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> ltr = ListsToRelations() >>> import pprint >>> instance = {‘o1’: {“list1”:[‘c’,’b’,’a’]}} >>> instance = ltr.transform(instance) >>> pprint.pprint(instance) {‘o1’: {‘list1’: {}},
(‘has-element’, (‘list1’, ‘o1’), ‘a’): True, (‘has-element’, (‘list1’, ‘o1’), ‘b’): True, (‘has-element’, (‘list1’, ‘o1’), ‘c’): True, (‘ordered-list’, (‘list1’, ‘o1’), ‘b’, ‘a’): True, (‘ordered-list’, (‘list1’, ‘o1’), ‘c’, ‘b’): True}>>> instance = ltr.undo_transform(instance) >>> pprint.pprint(instance) {'o1': {'list1': ['c', 'b', 'a']}}
-
class
concept_formation.preprocessor.NameStandardizer(gensym=None)[source]¶ Bases:
concept_formation.preprocessor.PreprocessorA preprocessor that standardizes apart object names.
Given an instance rename all the components so they have unique names.
This will rename component attributes as well as any occurance of the component’s name within relation attributes. This renaming is necessary to allow for a search between possible mappings without collisions.
This is the first operation in
StructureMapper’s standard pipeline.Parameters: gensym (a function) – a function that returns unique object names (str) on each call. If None, then default_gensym()is used, which keeps a global object counter.# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> import pprint >>> instance = {‘nominal’: ‘v1’, ‘numeric’: 2.3, ‘c1’: {‘a1’: ‘v1’}, ‘?c2’: … {‘a2’: ‘v2’, ‘?c3’: {‘a3’: ‘v3’}}, ‘(relation1 c1 ?c2)’: … True, ‘lists’: [{‘c1’: {‘inner’: ‘val’}}, ‘s2’, ‘s3’], … ‘(relation2 (a1 c1) (relation3 (a3 (?c3 ?c2))))’: 4.3, … (‘relation4’, ‘?c2’, ‘?c4’):True} >>> tuplizer = Tuplizer() >>> instance = tuplizer.transform(instance) >>> std = NameStandardizer() >>> std.undo_transform(instance) Traceback (most recent call last):
…Exception: Must call transform before undo_transform! >>> new_i = std.transform(instance) >>> old_i = std.undo_transform(new_i) >>> pprint.pprint(instance) {‘?c2’: {‘?c3’: {‘a3’: ‘v3’}, ‘a2’: ‘v2’},
‘c1’: {‘a1’: ‘v1’}, ‘lists’: [{‘c1’: {‘inner’: ‘val’}}, ‘s2’, ‘s3’], ‘nominal’: ‘v1’, ‘numeric’: 2.3, (‘relation1’, ‘c1’, ‘?c2’): True, (‘relation2’, (‘a1’, ‘c1’), (‘relation3’, (‘a3’, (‘?c3’, ‘?c2’)))): 4.3, (‘relation4’, ‘?c2’, ‘?c4’): True}>>> pprint.pprint(new_i) {'?o1': {'?o2': {'a3': 'v3'}, 'a2': 'v2'}, 'c1': {'a1': 'v1'}, 'lists': [{'c1': {'inner': 'val'}}, 's2', 's3'], 'nominal': 'v1', 'numeric': 2.3, ('relation1', 'c1', '?o1'): True, ('relation2', ('a1', 'c1'), ('relation3', ('a3', ('?o2', '?o1')))): 4.3, ('relation4', '?o1', '?o3'): True} >>> pprint.pprint(old_i) {'?c2': {'?c3': {'a3': 'v3'}, 'a2': 'v2'}, 'c1': {'a1': 'v1'}, 'lists': [{'c1': {'inner': 'val'}}, 's2', 's3'], 'nominal': 'v1', 'numeric': 2.3, ('relation1', 'c1', '?c2'): True, ('relation2', ('a1', 'c1'), ('relation3', ('a3', ('?c3', '?c2')))): 4.3, ('relation4', '?c2', '?c4'): True}
-
class
concept_formation.preprocessor.NominalToNumeric(on_fail=u'break', *attrs)[source]¶ Bases:
concept_formation.preprocessor.OneWayPreprocessorConverts nominal values to numeric ones.
Cobweb3andTrestlewill treat anything that passesisinstance(instance[attr],Number)as a numerical value. Because of how they store numerical distribution information, If either algorithm encounts a numerical value where it previously saw a nominal one it will throw an error. This preprocessor is provided as a way to address that problem by unifying the value types of attributes across an instance.Because parsing numbers is a less automatic function than casting things to strings this preprocessor has an extra parameter from
NumericToNominal. The on_fail parameter determines what should be done in the event of a parsing error and provides 3 options:'break'- Simply raises the ValueError that caused the problem and fails. (Default)'drop'- Drops any attributes that fail to parse. They would be treated as missing by categorization.'zero'- Replaces any problem values with0.0.
This is a helper function preprocessor and so is not part of
StructureMapper’s standard pipeline.>>> import pprint >>> ntn = NominalToNumeric() >>> instance = {"a":"123","b":"12.1241","c":"134"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'a': 123.0, 'b': 12.1241, 'c': 134.0}
>>> ntn = NominalToNumeric(on_fail='break') >>> instance = {"a":"123","b":"12.1241","c":"bad"} >>> instance = ntn.transform(instance) Traceback (most recent call last): ... ValueError: could not convert string to float: 'bad'
>>> ntn = NominalToNumeric(on_fail="drop") >>> instance = {"a":"123","b":"12.1241","c":"bad"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'a': 123.0, 'b': 12.1241}
>>> ntn = NominalToNumeric(on_fail="zero") >>> instance = {"a":"123","b":"12.1241","c":"bad"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'a': 123.0, 'b': 12.1241, 'c': 0.0}
>>> ntn = NominalToNumeric("break","a","b") >>> instance = {"a":"123","b":"12.1241","c":"bad"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'a': 123.0, 'b': 12.1241, 'c': 'bad'}
Parameters: - on_fail ('break', 'drop', or 'zero') – defines what should be done in the event of a numerical parse error
- attrs (strings) – A list of specific attributes to convert. If left empty all non-component values will be converted.
-
class
concept_formation.preprocessor.NumericToNominal(*attrs)[source]¶ Bases:
concept_formation.preprocessor.OneWayPreprocessorConverts numeric values to nominal ones.
Cobweb3andTrestlewill treat anything that passesisinstance(instance[attr],Number)as a numerical value. Because of how they store numerical distribution information, If either algorithm encounts a numerical value where it previously saw a nominal one it will throw an error. This preprocessor is provided as a way to address that problem by unifying the value types of attributes across an instance.This is a helper function preprocessor and so is not part of
StructureMapper’s standard pipeline.>>> import pprint >>> ntn = NumericToNominal() >>> instance = {"x":12.5,"y":9,"z":"top"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'x': '12.5', 'y': '9', 'z': 'top'}
>>> ntn = NumericToNominal("y") >>> instance = {"x":12.5,"y":9,"z":"top"} >>> instance = ntn.transform(instance) >>> pprint.pprint(instance) {'x': 12.5, 'y': '9', 'z': 'top'}
Parameters: attrs (strings) – A list of specific attributes to convert. If left empty all numeric values will be converted.
-
class
concept_formation.preprocessor.ObjectVariablizer(*attrs)[source]¶ Bases:
concept_formation.preprocessor.OneWayPreprocessorConverts all attributes with dictionary values into variables by adding a question mark.
Attribute names beginning with ? are treated as bindable variables while all other attributes names are considered constants. This process searches through an instances and variablizes attributes that might not have been defined this way in the original data.
This is a helper function preprocessor and so is not part of
StructureMapper’s standard pipeline.>>> from pprint import pprint >>> instance = {"ob1":{"myX":12.4,"myY":13.1,"myType":"square"},"ob2":{"myX":9.5,"myY":12.6,"myType":"rect"}} >>> ov = ObjectVariablizer() >>> instance = ov.transform(instance) >>> pprint(instance) {'?ob1': {'myType': 'square', 'myX': 12.4, 'myY': 13.1}, '?ob2': {'myType': 'rect', 'myX': 9.5, 'myY': 12.6}} >>> instance = ov.undo_transform(instance) >>> pprint(instance) {'?ob1': {'myType': 'square', 'myX': 12.4, 'myY': 13.1}, '?ob2': {'myType': 'rect', 'myX': 9.5, 'myY': 12.6}} >>> instance = {"p1":{"x":12,"y":3},"p2":{"x":5,"y":14},"p3":{"x":4,"y":18},"setttings":{"x_lab":"height","y_lab":"age"}} >>> ov = ObjectVariablizer("p1","p2","p3") >>> instance = ov.transform(instance) >>> pprint(instance) {'?p1': {'x': 12, 'y': 3}, '?p2': {'x': 5, 'y': 14}, '?p3': {'x': 4, 'y': 18}, 'setttings': {'x_lab': 'height', 'y_lab': 'age'}}
Parameters: attrs (strings) – A list of specific attribute names to variablize. If left empty then all variables will be converted.
-
class
concept_formation.preprocessor.OneWayPreprocessor[source]¶ Bases:
concept_formation.preprocessor.PreprocessorA template class that defines a transformation function that only works in the forward direction. If undo_transform is called then an exact copy of the given object is returned.
-
class
concept_formation.preprocessor.Pipeline(*preprocessors)[source]¶ Bases:
concept_formation.preprocessor.PreprocessorA special preprocessor class used to chain together many preprocessors. Supports the same transform and undo_transform functions as a regular preprocessor.
-
class
concept_formation.preprocessor.Preprocessor[source]¶ Bases:
objectA template class that defines the functions a preprocessor class should implement. In particular, a preprocessor should tranform an instance and implement a function for undoing this transformation.
-
class
concept_formation.preprocessor.Sanitizer(spec=u'trestle')[source]¶ Bases:
concept_formation.preprocessor.OneWayPreprocessorThis is a preprocessor that santizes instances to adhere to the general expectations of either Cobweb, Cobweb3 or Trestle. In general this means enforcing that attribute keys are either of type str or tuple and that relational tuples contain only values of str or tuple. The main reason for having this preprocessor is because many other things are valid dictionary keys in python and its possible to have weird behavior as a result.
>>> from pprint import pprint >>> instance = {'a1':'v1','a2':2,'a3':{'aa1':'1','aa2':2},1:'v2',len:'v3',('r1',2,'r3'):'v4',('r4','r5'):{'aa3':4,3:'v6'}} >>> pprint(instance) {<built-in function len>: 'v3', 1: 'v2', 'a1': 'v1', 'a2': 2, 'a3': {'aa1': '1', 'aa2': 2}, ('r1', 2, 'r3'): 'v4', ('r4', 'r5'): {3: 'v6', 'aa3': 4}} >>> san = Sanitizer('cobweb') >>> inst = san.transform(instance) >>> pprint(inst) {'1': 'v2', '<built-in function len>': 'v3', 'a1': 'v1', 'a2': 2, 'a3': "{'aa1':'1','aa2':2}", ('r1', 2, 'r3'): 'v4', ('r4', 'r5'): "{3:'v6','aa3':4}"} >>> san = Sanitizer('trestle') >>> inst = san.transform(instance) >>> pprint(inst) {'1': 'v2', '<built-in function len>': 'v3', 'a1': 'v1', 'a2': 2, 'a3': {'aa1': '1', 'aa2': 2}, ('r1', '2', 'r3'): 'v4', ('r4', 'r5'): {'3': 'v6', 'aa3': 4}}
-
class
concept_formation.preprocessor.SubComponentProcessor[source]¶ Bases:
concept_formation.preprocessor.PreprocessorTakes a flattened instance and moves sub-objects (not sub-attributes) to be top-level objects and adds has-component relations to preserve semantics.
This process is primairly used to improve matching by having all sub- component objects exist as their own top level objects with relations describing their original position in the hierarchy. This allows the structure mapper to partially match against subobjects.
This is the second operation in
TrestleTree’s standard pipeline (after flattening).Warning
This assumes that the
NameStandardizerhas been run on the instance first otherwise there can be name collisions.# Reset the symbol generator for doctesting purposes. >>> _reset_gensym() >>> import pprint >>> flattener = Flattener() >>> psc = SubComponentProcessor() >>> instance = {“a1”: “v1”, “?sub1”: {“a2”: “v2”, “a3”: 3}, … “?sub2”: {“a4”: “v4”, “?subsub1”: {“a5”: “v5”, “a6”: “v6”}, … “?subsub2”:{“?subsubsub”: {“a8”: “V8”}, “a7”: 7}}, … (‘ordered-list’, (‘list1’, (‘?o2’, ‘?o1’)), ‘b’, ‘a’): … True} >>> pprint.pprint(instance) {‘?sub1’: {‘a2’: ‘v2’, ‘a3’: 3},
- ‘?sub2’: {‘?subsub1’: {‘a5’: ‘v5’, ‘a6’: ‘v6’},
- ‘?subsub2’: {‘?subsubsub’: {‘a8’: ‘V8’}, ‘a7’: 7}, ‘a4’: ‘v4’},
‘a1’: ‘v1’, (‘ordered-list’, (‘list1’, (‘?o2’, ‘?o1’)), ‘b’, ‘a’): True}
>>> instance = psc.transform(flattener.transform(instance)) >>> pprint.pprint(instance) {'a1': 'v1', ('a2', '?sub1'): 'v2', ('a3', '?sub1'): 3, ('a4', '?sub2'): 'v4', ('a5', '?subsub1'): 'v5', ('a6', '?subsub1'): 'v6', ('a7', '?subsub2'): 7, ('a8', '?subsubsub'): 'V8', ('has-component', '?o1', '?o2'): True, ('has-component', '?sub2', '?subsub1'): True, ('has-component', '?sub2', '?subsub2'): True, ('has-component', '?subsub2', '?subsubsub'): True, ('ordered-list', ('list1', '?o2'), 'b', 'a'): True} >>> instance = psc.undo_transform(instance) >>> instance = flattener.undo_transform(instance) >>> pprint.pprint(instance) {'?sub1': {'a2': 'v2', 'a3': 3}, '?sub2': {'?subsub1': {'a5': 'v5', 'a6': 'v6'}, '?subsub2': {'?subsubsub': {'a8': 'V8'}, 'a7': 7}, 'a4': 'v4'}, 'a1': 'v1', ('ordered-list', ('list1', ('?o2', '?o1')), 'b', 'a'): True}
-
class
concept_formation.preprocessor.Tuplizer[source]¶ Bases:
concept_formation.preprocessor.PreprocessorConverts all string versions of relations into tuples.
Relation attributes are expected to be specified as a string enclosed in
()with values delimited by spaces. We conventionally use a prefix notation for relations(related a b)but this preprocessor should be flexible enough to handle postfix and prefix.This is a helper function preprocessor and so is not part of
StructureMapper’s standard pipeline.>>> tuplizer = Tuplizer() >>> instance = {'(foo1 o1 (foo2 o2 o3))': True} >>> print(tuplizer.transform(instance)) {('foo1', 'o1', ('foo2', 'o2', 'o3')): True} >>> print(tuplizer.undo_transform(tuplizer.transform(instance))) {'(foo1 o1 (foo2 o2 o3))': True}
>>> instance = {'(place x1 12.4 9.6 (div width 18.2))':True} >>> tuplizer = Tuplizer() >>> tuplizer.transform(instance) {('place', 'x1', 12.4, 9.6, ('div', 'width', 18.2)): True}
-
concept_formation.preprocessor.default_gensym()[source]¶ Generates unique names for naming renaming apart objects.
Returns: a unique object name Return type: ‘o’+counter
-
concept_formation.preprocessor.get_attribute_components(attribute, vars_only=True)[source]¶ Gets component names out of an attribute
>>> from pprint import pprint >>> attr = ('a', ('sub1', '?c1')) >>> get_attribute_components(attr) {'?c1'}
>>> attr = '?c1' >>> get_attribute_components(attr) {'?c1'}
>>> attr = ('a', ('sub1', 'c1')) >>> get_attribute_components(attr) set()
>>> attr = 'c1' >>> get_attribute_components(attr) set()
-
concept_formation.preprocessor.rename_relation(relation, mapping)[source]¶ Takes a tuplized relational attribute (e.g.,
('before', 'o1', 'o2')) and a mapping and renames the components based on the mapping. This function contains a special edge case for handling dot notation which is used in the NameStandardizer.Parameters: - attr (Relation Attribute) – The relational attribute containing components to be renamed
- mapping (dict) – A dictionary of mappings between component names
Returns: A new relational attribute with components renamed
Return type: tuple
>>> relation = ('foo1', 'o1', ('foo2', 'o2', 'o3')) >>> mapping = {'o1': 'o100', 'o2': 'o200', 'o3': 'o300'} >>> rename_relation(relation, mapping) ('foo1', 'o100', ('foo2', 'o200', 'o300'))
>>> relation = ('foo1', ('o1', ('o2', 'o3'))) >>> mapping = {('o1', ('o2', 'o3')): 'o100'} >>> rename_relation(relation, mapping) ('foo1', 'o100')
concept_formation.continuous_value module¶
-
class
concept_formation.continuous_value.ContinuousValue[source]¶ This class is used to store the number of samples, the mean of the samples, and the squared error of the samples for Numeric Values. It can be used to perform incremental estimation of the attribute’s mean, std, and unbiased std.
Initially the number of values, the mean of the values, and the squared errors of the values are set to 0.
-
biased_std()[source]¶ Returns a biased estimate of the std (i.e., the sample std)
Returns: biased estimate of the std (i.e., the sample std) Return type: float
-
combine(other)[source]¶ Combine another ContinuousValue’s distribution into this one in an efficient and practical (no precision problems) way.
This uses the parallel algorithm by Chan et al. found at: https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm
Parameters: other (ContinuousValue) – Another ContinuousValue distribution to be incorporated into this one.
-
copy()[source]¶ Returns a deep copy of itself.
Returns: a deep copy of the continuous value Return type: ContinuousValue
-
integral_of_gaussian_product(other)[source]¶ Computes the integral (from -inf to inf) of the product of two gaussians. It adds gaussian noise to both stds, so that the integral of their product never exceeds 1.
- Use formula computed here:
- http://www.tina-vision.net/docs/memos/2003-003.pdf
-
scaled_biased_std(scale)[source]¶ Returns an biased estimate of the std (see:
ContinuousValue.biased_std()), but also adjusts the std given a scale parameter.This is used to return std values that have been normalized by some value. For edge cases, if scale is less than or equal to 0, then scaling is disabled (i.e., scale = 1.0).
Parameters: scale (float) – an amount to scale biased std estimates by Returns: A scaled unbiased estimate of std Return type: float
-
scaled_unbiased_mean(shift, scale)[source]¶ Returns a shifted and scaled unbiased mean. This is equivelent to (self.unbiased_mean() - shift) / scale
This is used as part of numerical value scaling.
Parameters: - shift (float) – the amount to shift the mean by
- scale (float) – the amount to scale the returned mean by
Returns: (self.mean - shift) / scaleReturn type: float
-
scaled_unbiased_std(scale)[source]¶ Returns an unbiased estimate of the std (see:
ContinuousValue.unbiased_std()), but also adjusts the std given a scale parameter.This is used to return std values that have been normalized by some value. For edge cases, if scale is less than or equal to 0, then scaling is disabled (i.e., scale = 1.0).
Parameters: scale (float) – an amount to scale unbiased std estimates by Returns: A scaled unbiased estimate of std Return type: float
-
unbiased_mean()[source]¶ Returns an unbiased estimate of the mean.
Returns: the unbiased mean Return type: float
-
unbiased_std()[source]¶ Returns an unbiased estimate of the std, but for n < 2 the std is estimated to be 0.0.
This implementation uses Bessel’s correction and Cochran’s theorem: https://en.wikipedia.org/wiki/Unbiased_estimation_of_standard_deviation#Bias_correction
Returns: an unbiased estimate of the std Return type: float See also
-
update(x)[source]¶ Incrementally update the mean and squared mean error (meanSq) values in an efficient and practical (no precision problems) way.
This uses and algorithm by Knuth found here: https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance
Parameters: x (Number) – A new value to incorporate into the distribution
-
concept_formation.structure_mapper module¶
This module contains the
StructureMapper
class which is used rename variable attributes it improve the category utility
on instances.
It is an instance of a
preprocessor with a
transform() and undo_tranform() methods.
-
class
concept_formation.structure_mapper.StructureMapper(base)[source]¶ Bases:
concept_formation.preprocessor.PreprocessorStructure maps an instance that has been appropriately preprocessed (i.e., standardized apart, flattened, subcomponent processed, and lists processed out). Transform renames the instance based on this structure mapping, and return the renamed instance.
Parameters: - base (TrestleNode) – A concept to structure map the instance to
- gensym (function) – a function that returns unique object names (str) on each call
Returns: A flattened and mapped copy of the instance
Return type: instance
-
get_mapping()[source]¶ Returns the currently established mapping.
Returns: The current mapping. Return type: dict
-
transform(target, initial_mapping=None)[source]¶ Transforms a provided target (either an instance or an av_counts table from a CobwebNode or Cobweb3Node).
Parameters: target (instance or av_counts table (from CobwebNode or Cobweb3Node)) – An instance or av_counts table to rename to bring into alignment with the provided base. Returns: The renamed instance or av_counts table Return type: instance or av_counts table
-
undo_transform(target)[source]¶ Takes a transformed target and reverses the structure mapping using the mapping discovered by transform.
Parameters: target (previously structure mapped instance or av_counts table (from CobwebNode or Cobweb3Node)) – A previously renamed instance or av_counts table to reverse the structure mapping on. Returns: An instance or concept av_counts table with original object names Return type: dict
-
class
concept_formation.structure_mapper.StructureMappingOptimizationProblem(initial, goal=None, initial_cost=0, extra=None)[source]¶ Bases:
py_search.base.ProblemA class for describing a structure mapping problem to be solved using the py_search library. This class defines the node_value, the successor, and goal_test methods used by the search library.
Unlike StructureMappingProblem, this class uses a local search approach; i.e., given an initial mapping it tries to improve the mapping by permuting it.
-
random_successor(node)[source]¶ Similar to the successor function, but generates only a single random successor.
-
-
concept_formation.structure_mapper.bind_flat_attr(attr, mapping)[source]¶ Renames an attribute given a mapping.
Parameters: - attr (str or tuple) – The attribute to be renamed
- mapping (dict) – A dictionary of mappings between component names
- unnamed (dict) – A list of components that are not yet mapped.
Returns: The attribute’s new name or
Noneif the mapping is incompleteReturn type: str
>>> attr = ('before', '?c1', '?c2') >>> mapping = {'?c1': '?o1', '?c2':'?o2'} >>> bind_flat_attr(attr, mapping) ('before', '?o1', '?o2')
>>> attr = ('ordered-list', ('cells', '?obj12'), '?obj10', '?obj11') >>> mapping = {'?obj12': '?o1', '?obj10':'?o2', '?obj11': '?o3'} >>> bind_flat_attr(attr, mapping) ('ordered-list', ('cells', '?o1'), '?o2', '?o3')
If the mapping is incomplete then returns partially mapped attributes
>>> attr = ('before', '?c1', '?c2') >>> mapping = {'?c1': 'o1'} >>> bind_flat_attr(attr, mapping) ('before', 'o1', '?c2')
>>> bind_flat_attr(('<', ('a', '?o2'), ('a', '?o1')), {'?o1': '?c1'}) ('<', ('a', '?o2'), ('a', '?c1'))
>>> bind_flat_attr(('<', ('a', '?o2'), ('a', '?o1')), ... {'?o1': '?c1', '?o2': '?c2'}) ('<', ('a', '?c2'), ('a', '?c1'))
-
concept_formation.structure_mapper.contains_component(component, attr)[source]¶ Return
Trueif the given component name is in the attribute, either as part of a hierarchical name or within a relations otherwiseFalse.Parameters: - component (str) – A component name
- attr – An attribute name
Returns: Trueif the component name exists inside the attribute nameFalseotherwiseReturn type: bool
>>> contains_component('?c1', ('relation', '?c2', ('a', '?c1'))) True >>> contains_component('?c3', ('before', '?c1', '?c2')) False
-
concept_formation.structure_mapper.flat_match(target, base, initial_mapping=None)[source]¶ Given a base (usually concept) and target (instance or concept av table) this function returns a mapping that can be used to rename components in the target. Search is used to find a mapping that maximizes the expected number of correct guesses in the concept after incorporating the instance.
The current approach is to refine the initially provided mapping using a local hill-climbing search. If no initial mapping is provided then one is generated using the Munkres / Hungarian matching on object-to-object assignment (no relations). This initialization approach is polynomial in the size of the base.
Parameters: - target (Instance or av_counts obj from concept) – An instance or concept.av_counts object to be mapped to the base concept.
- base (TrestleNode) – A concept to map the target to
- initial_mapping (A mapping dict) – An initial mapping to seed the local search
Returns: a mapping for renaming components in the instance.
Return type: dict
-
concept_formation.structure_mapper.get_component_names(instance, vars_only=True)[source]¶ Given an instance or a concept’s probability table return a list of all of the component names. If vars_only is false, than all constants and variables are returned.
Parameters: - instance (an instance) – An instance or a concept’s probability table.
- vars_only (boolean) – Whether or not to return only variables (i.e., strings with a names with a ‘?’ at the beginning) or both variables and constants.
Returns: A frozenset of all of the component names present in the instance
Return type: frozenset
>>> instance = {('a', ('sub1', 'c1')): 0, ('a', 'c2'): 0, ... ('_', '_a', 'c3'): 0} >>> names = get_component_names(instance, False) >>> frozenset(names) == frozenset({'c3', 'c2', ('sub1', 'c1'), 'sub1', 'a', ... ('a', ('sub1', 'c1')), ('a', 'c2'), ... 'c1'}) True >>> names = get_component_names(instance, True) >>> frozenset(names) == frozenset() True
>>> instance = {('relation1', ('sub1', 'c1'), 'o3'): True} >>> names = get_component_names(instance, False) >>> frozenset(names) == frozenset({'o3', ('relation1', ('sub1', 'c1'), ... 'o3'), 'sub1', ('sub1', 'c1'), ... 'c1', 'relation1'}) True
-
concept_formation.structure_mapper.hungarian_mapping(inames, cnames, target, base)[source]¶ Utilizes the hungarian/munkres matching algorithm to compute an initial mapping of inames to cnames. The base cost is the expected correct guesses if each object is matched to itself (i.e., a new object). Then the cost of each object-object match is evaluated by setting each individual object and computing the expected correct guesses.
Parameters: - inames (collection) – the target component names
- cnames (collection) – the base component names
- target (Instance or av_counts obj from concept) – An instance or concept.av_counts object to be mapped to the base concept.
- base (TrestleNode) – A concept to map the target to
Returns: a mapping for renaming components in the instance.
Return type: frozenset
-
concept_formation.structure_mapper.is_partial_match(iAttr, cAttr, mapping)[source]¶ Returns True if the instance attribute (iAttr) partially matches the concept attribute (cAttr) given the mapping.
Parameters: - iAttr (str or tuple) – An attribute in an instance
- cAttr (str or tuple) – An attribute in a concept
- mapping (dict) – A mapping between between attribute names
- unnamed (dict) – A list of components that are not yet mapped.
Returns: Trueif the instance attribute matches the concept attribute in the mapping otherwiseFalseReturn type: bool
>>> is_partial_match(('<', ('a', '?o2'), ('a', '?o1')), ... ('<', ('a', '?c2'), ('b', '?c1')), {'?o1': '?c1'}) False
>>> is_partial_match(('<', ('a', '?o2'), ('a', '?o1')), ... ('<', ('a', '?c2'), ('a', '?c1')), {'?o1': '?c1'}) True
>>> is_partial_match(('<', ('a', '?o2'), ('a', '?o1')), ... ('<', ('a', '?c2'), ('a', '?c1')), ... {'?o1': '?c1', '?o2': '?c2'}) True
-
concept_formation.structure_mapper.mapping_cost(mapping, target, base)[source]¶ Used to evaluate a mapping between a target and a base. This is performed by renaming the target using the mapping, adding it to the base and evaluating the expected number of correct guesses in the newly updated concept.
Parameters: - mapping (frozenset or dict) – the mapping of target items to base items
- target (an instance or concept.av_counts) – the target
- base (a concept) – the base
-
concept_formation.structure_mapper.rename_flat(target, mapping)[source]¶ Given an instance and a mapping rename the components and relations and return the renamed instance.
Parameters: - instance (instance) – An instance to be renamed according to a mapping
- mapping (dict) –
param mapping: A dictionary of mappings between component names
Returns: A copy of the instance with components and relations renamed
Return type: instance
>>> import pprint >>> instance = {('a', '?c1'): 1, ('good', '?c1'): True} >>> mapping = {'?c1': '?o1'} >>> renamed = rename_flat(instance,mapping) >>> pprint.pprint(renamed) {('a', '?o1'): 1, ('good', '?o1'): True}
concept_formation.datasets module¶
The dataset module has functions for loading a variety of datasets that are properly formated for use with CobwebTrees and their derivatives.
-
concept_formation.datasets.load_congressional_voting(num_instances=None)[source]¶ Load the voting dataset.
This is an example of instances with only Nominal values and Constant attributes but some attributes are occasionally missing. This dataset contains 435 instances.
This dataset was downloaded from the UCI machine learning repository. We processed the data to be in dictionary format with human readable labels.
>>> import pprint >>> data = load_congressional_voting(num_instances=1) >>> pprint.pprint(data[0]) {'Class Name': 'republican', 'adoption-of-the-budget-resolution': 'n', 'aid-to-nicaraguan-contras': 'n', 'anti-satellite-test-ban': 'n', 'crime': 'y', 'duty-free-exports': 'n', 'education-spending': 'y', 'el-salvador-aid': 'y', 'export-administration-act-south-africa': 'y', 'handicapped-infants': 'n', 'immigration': 'y', 'mx-missile': 'n', 'physician-fee-freeze': 'y', 'religious-groups-in-schools': 'y', 'superfund-right-to-sue': 'y', 'water-project-cost-sharing': 'y'}
-
concept_formation.datasets.load_forest_fires(num_instances=None)[source]¶ Load the forest fires dataset.
This is an example of instances with Nominal and Numeric values and Constant attributes. This dataset contains 517 instances.
This dataset was downloaded from the UCI machine learning repository. We processed the data to be in dictionary format with human readable labels.
>>> import pprint >>> data = load_forest_fires(num_instances=1) >>> pprint.pprint(data[0]) {'DC': 94.3, 'DMC': 26.2, 'FFMC': 86.2, 'ISI': 5.1, 'RH': 51.0, 'area': 0.0, 'day': 'fri', 'month': 'mar', 'rain': 0.0, 'temp': 8.2, 'wind': 6.7, 'x-axis': 7.0, 'y-axis': 5.0}
-
concept_formation.datasets.load_iris(num_instances=None)[source]¶ Load the iris dataset.
This is an example of instances with Nominal and Numeric values and Constant attributes. This dataset contains 150 instances.
This dataset was downloaded from the UCI machine learning repository. We processed the data to be in dictionary format with human readable labels.
>>> import pprint >>> data = load_iris(num_instances=1) >>> pprint.pprint(data[0]) {'class': 'Iris-setosa', 'petal length': 1.4, 'petal width': 0.2, 'sepal length': 5.1, 'sepal width': 3.5}
-
concept_formation.datasets.load_molecule(num_instances=None)[source]¶ Load a dataset of 101 molecules from the pubchem database
This dataset was downloaded from the Pubchem databse. We used a custom `molfile parser<https://github.com/eharpste/molparser>`__ to process the data to be in dictionary format with human readable labels.
>>> import pprint >>> data = load_molecule() >>> pprint.pprint(data[3]) {'(bond Single Not_stereo ?atom0001 ?atom0003)': True, '(bond Single Not_stereo ?atom0001 ?atom0014)': True, '(bond Single Not_stereo ?atom0002 ?atom0004)': True, '(bond Single Not_stereo ?atom0002 ?atom0012)': True, '(bond Single Not_stereo ?atom0002 ?atom0013)': True, '(bond Single Not_stereo ?atom0003 ?atom0004)': True, '(bond Single Not_stereo ?atom0003 ?atom0005)': True, '(bond Single Not_stereo ?atom0003 ?atom0006)': True, '(bond Single Not_stereo ?atom0004 ?atom0007)': True, '(bond Single Not_stereo ?atom0004 ?atom0008)': True, '(bond Single Not_stereo ?atom0005 ?atom0009)': True, '(bond Single Not_stereo ?atom0005 ?atom0010)': True, '(bond Single Not_stereo ?atom0005 ?atom0011)': True, '?atom0001': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'O', 'valence': 'no marking', 'x': 2.5369, 'y': 0.75, 'z': 0.0}, '?atom0002': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'N', 'valence': 'no marking', 'x': 5.135, 'y': 0.25, 'z': 0.0}, '?atom0003': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'unmarked', 'symbol': 'C', 'valence': 'no marking', 'x': 3.403, 'y': 0.25, 'z': 0.0}, '?atom0004': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'C', 'valence': 'no marking', 'x': 4.269, 'y': 0.75, 'z': 0.0}, '?atom0005': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'C', 'valence': 'no marking', 'x': 3.403, 'y': -0.75, 'z': 0.0}, '?atom0006': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 3.403, 'y': 1.1, 'z': 0.0}, '?atom0007': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 4.6675, 'y': 1.225, 'z': 0.0}, '?atom0008': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 3.8705, 'y': 1.225, 'z': 0.0}, '?atom0009': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 2.783, 'y': -0.75, 'z': 0.0}, '?atom0010': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 3.403, 'y': -1.37, 'z': 0.0}, '?atom0011': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 4.023, 'y': -0.75, 'z': 0.0}, '?atom0012': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 5.672, 'y': 0.56, 'z': 0.0}, '?atom0013': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 5.135, 'y': -0.37, 'z': 0.0}, '?atom0014': {'charge': 'outside_limits', 'hydrogen_count': 'H0', 'mass_diff': '0', 'stereo_parity': 'not_stereo', 'symbol': 'H', 'valence': 'no marking', 'x': 2.0, 'y': 0.44, 'z': 0.0}, '_name': '4', '_software': '-OEChem-03201502492D', '_version': 'V2000', 'chiral': True}
-
concept_formation.datasets.load_mushroom(num_instances=None)[source]¶ Load the mushroom dataset.
This is an example of instances with only Nominal values and Constant attributes. This dataset contains 8124 instances.
This dataset was downloaded from the UCI machine learning repository. We processed the data to be in dictionary format with human readable labels.
>>> import pprint >>> data = load_mushroom(num_instances=1) >>> pprint.pprint(data[0]) {'bruises?': 'yes', 'cap-color': 'brown', 'cap-shape': 'convex', 'cap-surface': 'smooth', 'classification': 'poisonous', 'gill-attachment': 'free', 'gill-color': 'black', 'gill-size': 'narrow', 'gill-spacing': 'closed', 'habitat': 'urban', 'odor': 'pungent', 'population': 'scattered', 'ring-number': 'one', 'ring-type': 'pendant', 'spore-print-color': 'black', 'stalk-color-above-ring': 'white', 'stalk-color-below-ring': 'white', 'stalk-root': 'equal', 'stalk-shape': 'enlarging', 'stalk-surface-above-ring': 'smooth', 'stalk-surface-below-ring': 'smooth', 'veil-color': 'white', 'veil-type': 'partial'}
-
concept_formation.datasets.load_quadruped(num_instances)[source]¶ Returns a randomly generated quadruped dataset of size num_instances using the procedure employed in:
Gennari, J. H., Langley, P., & Fisher, D. H. (1989). Models of incremental concept formation. Artificial Intelligence, 40, 11-61.
This dataset contains four kinds of quadruped animals: dogs, cats, horses, and giraffes. The type of each component is included as a hidden variable, so that structure mapping can be tested. Additionally, the type of animal (e.g., dog) is also included as a hidden variable.
>>> import pprint >>> import random >>> random.seed(0) >>> data = load_quadruped(10) >>> print(len(data)) 10 >>> pprint.pprint(data[0:1]) [{'_type': 'giraffe', 'head': {'_type': 'head', 'axisX': 1, 'axisY': -0.23376215459531377, 'axisZ': 0, 'height': 19.069373148228724, 'locationX': 71.71171645023995, 'locationY': 0, 'locationZ': 49.26645266304532, 'radius': 4.05626484907961, 'texture': 177.5670433982545}, 'leg1': {'_type': 'leg1', 'axisX': 0.25279896094692916, 'axisY': 0, 'axisZ': -1, 'height': 60.13197726212744, 'locationX': 35.29119556606559, 'locationY': 12.845931778870957, 'locationZ': -42.91192040993468, 'radius': 3.597944849223721, 'texture': 179.23727389536953}, 'leg2': {'_type': 'leg2', 'axisX': 0, 'axisY': 0, 'axisZ': -1, 'height': 60.13197726212744, 'locationX': 35.29119556606559, 'locationY': -12.845931778870957, 'locationZ': -42.91192040993468, 'radius': 2.009043416794043, 'texture': 174.58392827108403}, 'leg3': {'_type': 'leg3', 'axisX': 0, 'axisY': 0, 'axisZ': -1, 'height': 60.13197726212744, 'locationX': -35.29119556606559, 'locationY': 12.845931778870957, 'locationZ': -42.91192040993468, 'radius': 2.348946587645933, 'texture': 178.9283460962157}, 'leg4': {'_type': 'leg4', 'axisX': 0.28802829434429883, 'axisY': 0, 'axisZ': -1, 'height': 60.13197726212744, 'locationX': -35.29119556606559, 'locationY': -12.845931778870957, 'locationZ': -42.91192040993468, 'radius': 2.9029316087251233, 'texture': 171.86316987918838}, 'neck': {'_type': 'neck', 'axisX': 1, 'axisY': 0, 'axisZ': 1, 'height': 51.49861653022255, 'locationX': 53.50145600815277, 'locationY': 0, 'locationZ': 31.05619222095814, 'radius': 7.87732253394808, 'texture': 177.14627952379485}, 'tail': {'_type': 'tail', 'axisX': -1, 'axisY': 0.24883477194257322, 'axisZ': -0.531438665320418, 'height': 20.918101962779517, 'locationX': -49.66428916935166, 'locationY': 0, 'locationZ': 0, 'radius': 0.9455145384298446, 'texture': 177.24907471005645}, 'torso': {'_type': 'torso', 'axisX': 1, 'axisY': 0, 'axisZ': 0, 'height': 70.58239113213118, 'locationX': 0, 'locationY': 0, 'locationZ': 0, 'radius': 12.845931778870957, 'texture': 171.2283287965781}}]
-
concept_formation.datasets.load_rb_com_11()[source]¶ Load the RumbleBlocks, Center of Mass Level 11, dataset.
This is an example of instances with all the attribute and value types described in the Instance Representation. This dataset contains 251 instances.
>>> import pprint >>> data = load_rb_com_11() >>> pprint.pprint(data[0]) {'_guid': 'ea022d3d-5c9e-46d7-be23-8ea718fe7816', '_human_cluster_label': '0', 'component0': {'b': 1.0, 'l': 0.0, 'r': 1.0, 't': 2.0, 'type': 'cube0'}, 'component1': {'b': 3.0, 'l': 2.0, 'r': 3.0, 't': 4.0, 'type': 'cube0'}, 'component14': {'b': 4.0, 'l': 1.0, 'r': 4.0, 't': 5.0, 'type': 'ufoo0'}, 'component2': {'b': 1.0, 'l': 1.0, 'r': 4.0, 't': 2.0, 'type': 'plat0'}, 'component3': {'b': 2.0, 'l': 1.0, 'r': 4.0, 't': 3.0, 'type': 'plat0'}, 'component4': {'b': 0.0, 'l': 0.0, 'r': 5.0, 't': 1.0, 'type': 'rect0'}}
-
concept_formation.datasets.load_rb_s_07(num_instances=None)[source]¶ Load the RumbleBlocks, Symmetry Level 7, dataset.
This is an example of instances with all the attribute and value types described in the Instance Representation. This dataset contains 141 instances.
>>> import pprint >>> data = load_rb_s_07(num_instances=1) >>> pprint.pprint(data[0]) {'_guid': '660ac76d-93b3-4ce7-8a15-a3213e9103f5', 'component0': {'b': 0.0, 'l': 0.0, 'r': 3.0, 't': 1.0, 'type': 'plat0'}, 'component1': {'b': 1.0, 'l': 1.0, 'r': 2.0, 't': 4.0, 'type': 'plat90'}, 'component8': {'b': 4.0, 'l': 0.0, 'r': 3.0, 't': 5.0, 'type': 'ufoo0'}, 'success': '0'}
-
concept_formation.datasets.load_rb_s_07_human_predictions()[source]¶ Load the Human Predictions Data for the RumbleBlocks, Symmetry Level 7, dataset.
This is data collected from mechanical turk, where workers were tasked with predicting a concept label (success) given a picture of the tower. The element contains labels for the data and subsequent rows contain the actual data. This dataset contains 601 instances.
>>> import pprint >>> data = load_rb_s_07_human_predictions() >>> pprint.pprint(data[0:2]) ['user_id,instance_guid,time,order,prediction,correctness', '1,2fda0bde-95a7-4bda-9851-785275c3f56d,2015-02-15 ' '19:21:14.327344+00:00,1,0,1']
-
concept_formation.datasets.load_rb_s_13(num_instances=None)[source]¶ Load the RumbleBlocks, Symmetry Level 13, dataset.
This is an example of instances with all the attribute and value types described in the Instance Representation. This dataset contains 249 instances.
>>> import pprint >>> data = load_rb_s_13(num_instances=1) >>> pprint.pprint(data[0]) {'_guid': '684b4ce5-0f55-481c-ae9a-1474de8418ea', '_human_cluster_label': '0', 'component0': {'b': 3.0, 'l': 2.0, 'r': 3.0, 't': 4.0, 'type': 'cube0'}, 'component1': {'b': 4.0, 'l': 2.0, 'r': 3.0, 't': 5.0, 'type': 'cube0'}, 'component14': {'b': 0.0, 'l': 0.0, 'r': 4.0, 't': 1.0, 'type': 'trap0'}, 'component15': {'b': 5.0, 'l': 1.0, 'r': 3.0, 't': 6.0, 'type': 'ufoo0'}, 'component2': {'b': 1.0, 'l': 0.0, 'r': 3.0, 't': 2.0, 'type': 'plat0'}, 'component3': {'b': 2.0, 'l': 0.0, 'r': 3.0, 't': 3.0, 'type': 'plat0'}}
-
concept_formation.datasets.load_rb_wb_03(num_instances=None)[source]¶ Load the RumbleBlocks, Wide Base Level 03, dataset.
This is an example of instances with all the attribute and value types described in the Instance Representation. This dataset contains 254 instances.
>>> import pprint >>> data = load_rb_wb_03(num_instances=1) >>> pprint.pprint(data[0]) {'_guid': 'aa5eff72-0572-4eff-a007-3def9a82ba5b', '_human_cluster_label': '0', 'component0': {'b': 2.0, 'l': 2.0, 'r': 3.0, 't': 3.0, 'type': 'cube0'}, 'component1': {'b': 2.0, 'l': 3.0, 'r': 4.0, 't': 3.0, 'type': 'cube0'}, 'component11': {'b': 3.0, 'l': 1.0, 'r': 4.0, 't': 4.0, 'type': 'ufoo0'}, 'component2': {'b': 1.0, 'l': 2.0, 'r': 5.0, 't': 2.0, 'type': 'plat0'}, 'component3': {'b': 0.0, 'l': 0.0, 'r': 5.0, 't': 1.0, 'type': 'rect0'}}
concept_formation.visualize module¶
The visualize module provides functions for generating html visualizations of trees created by the other modules of concept_formation.
-
concept_formation.visualize.visualize(tree, dst=None, recreate_html=True)[source]¶ Create an interactive visualization of a concept_formation tree and open it in your browswer.
If a destination directory is specified this function will create html, js, and css files in the destination directory provided. By default this will always recreate the support html, js, and css files but a flag can turn this off.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to visualize - dst (str) – A directory to generate visualization files into. If None no files will be generated
- create_html (bool) – A flag for whether new supporting html files should be created
- tree (
-
concept_formation.visualize.visualize_clusters(tree, clusters, dst=None, recreate_html=True)[source]¶ Create an interactive visualization of a concept_formation tree trimmed to the level specified by a clustering from the cluster module.
This visualization differs from the normal one by trimming the tree to the level of a clustering. Basically the output traverses down the tree but stops recursing if it hits a node in the clustering. Both label or concept based clusterings are supported as the relevant names will be extracted.
If a destination directory is specified this function will create html, js, and css files in the destination directory provided. By default this will always recreate the support html, js, and css files but a flag can turn this off.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to visualize - clusters (list) – A list of cluster labels or concept nodes generated by the cluster module.
- dst (str) – A directory to generate visualization files into. If None no files will be generated
- create_html (bool) – A flag for whether new supporting html files should be created
- tree (
-
concept_formation.visualize.visualize_no_leaves(tree, cuts=1, dst=None, recreate_html=True)[source]¶ Create an interactive visualization of a concept_formation tree cuts levels above the leaves and open it in your browswer.
This visualization differs from the normal one by trimming the leaves from the tree. This is often useful in seeing patterns when the individual leaves are overly frequent visual noise.
If a destination directory is specified this function will create html, js, and css files in the destination directory provided. By default this will always recreate the support html, js, and css files but a flag can turn this off.
Parameters: - tree (
CobwebTree,Cobweb3Tree, orTrestleTree) – A category tree to visualize - cuts (int) – The number of times to trim up the leaves
- dst (str) – A directory to generate visualization files into. If None no files will be generated
- create_html (bool) – A flag for whether new supporting html files should be created
- tree (
concept_formation.utils module¶
The utils module contains a number of utility functions used by other modules.
-
concept_formation.utils.c4(n)[source]¶ Returns the correction factor to apply to unbias estimates of standard deviation in low sample sizes. This implementation is based on a lookup table for n in [2-29] and returns 1.0 for values >= 30.
>>> c4(3) 0.886226925452758
-
concept_formation.utils.isNumber(n)[source]¶ Check if a value is a number that should be handled differently than nominals.
-
concept_formation.utils.mean(values)[source]¶ Computes the mean of a list of values.
This is primarily included to reduce dependency on external math libraries like numpy in the core algorithm.
Parameters: values (list) – a list of numbers Returns: the mean of the list of values Return type: float >>> mean([600, 470, 170, 430, 300]) 394.0
-
concept_formation.utils.most_likely_choice(choices)[source]¶ Given a list of tuples [(val, prob),…(val, prob)], returns the value with the highest probability. Ties are randomly broken.
>>> options = [('a',.25),('b',.12),('c',.46),('d',.07)] >>> most_likely_choice(options) 'c' >>> most_likely_choice(options) 'c' >>> most_likely_choice(options) 'c'
Parameters: choices ([(val, prob),..(val, prob)]) – A list of tuples Returns: the val with the hightest prob Return type: val
-
concept_formation.utils.std(values)[source]¶ Computes the standard deviation of a list of values.
This is primarily included to reduce dependency on external math libraries like numpy in the core algorithm.
Parameters: values (list) – a list of numbers Returns: the standard deviation of the list of values Return type: float >>> std([600, 470, 170, 430, 300]) 147.32277488562318
-
concept_formation.utils.weighted_choice(choices)[source]¶ Given a list of tuples [(val, prob),…(val, prob)], return a randomly chosen value where the choice is weighted by prob.
Parameters: choices ([(val, prob),..(val, prob)]) – A list of tuples Returns: A choice sampled from the list according to the weightings Return type: val >>> from random import seed >>> seed(1234) >>> options = [('a',.25),('b',.12),('c',.46),('d',.07)] >>> weighted_choice(options) 'd' >>> weighted_choice(options) 'c' >>> weighted_choice(options) 'a'
See also
CobwebNode.sample
concept_formation.dummy module¶
The dummy module contains the DummyTree class, which can be used as a
naive baseline for comparison against CobwebTrees. This class makes predictions
based on the overall average of instances it has seen.
-
class
concept_formation.dummy.DummyTree[source]¶ Bases:
concept_formation.trestle.TrestleTreeThe DummyTree is designed to serve as a naive baseline to compare
Trestleto. The DummyTree can performstructure mappingbut in all other respects it is effectively a tree that consists of only a root.-
categorize(instance)[source]¶ Return the root of the tree. Because the DummyTree contains only 1 node then it will always categorize instances to that node.
This process does not modify the tree’s knoweldge. For a modifying version see:
DummyTree.ifit().Parameters: instance (Instance) – an instance to be categorized into the tree. Returns: the root node of the tree containing everything ever added to it. Return type: Cobweb3Node
-
gensym()[source]¶ Generates unique names for naming renaming apart objects.
Returns: a unique object name Return type: ‘?o’+counter
-
ifit(instance, do_mapping=False)[source]¶ Just maintain a set of counts at the root and use these for prediction.
The structure_map parameter determines whether or not to do structure mapping. This is disabled by default to get a really naive model.
This process modifies the tree’s knoweldge. For a non-modifying version see:
DummyTree.categorize().Parameters: - instance (Instance) – an instance to be categorized into the tree.
- do_mapping (bool) – a flag for whether or not to do structure mapping.
Returns: the root node of the tree containing everything ever added to it.
Return type:
-